Teori om automater, endelige automater
Strukturen, designen, operasjonsprinsippet til forskjellige maskiner bestemmes i stor grad av dets funksjonelle formål. Skille mellom teknologiske, transport, databehandling, militære og andre maskiner. Hele automatiske komplekser designet for å utføre komplekse teknologiske prosesser er mye introdusert i ulike bransjer. Automater er designet og bygget som utfører ulike logiske funksjoner (logiske maskiner).
Teori om automater — kybernetikkseksjonen, som oppsto under påvirkning av kravene til teknologien til digitale datamaskiner og kontrollmaskiner. Diskrete automater studert i automatteori er abstrakte modeller av virkelige systemer (både tekniske og biologiske) som behandler diskret (digital) informasjon på diskrete tidstrinn.
Automateteori er basert på presise matematiske konsepter som formaliserer intuitive ideer om funksjonen (atferden) til automaten og om dens struktur (intern struktur).
I dette tilfellet er informasjonstransformasjon alltid forstått som en operasjon som transformerer inngangssekvenser sammensatt av bokstaver fra inngangsalfabetet til utgangssekvenser sammensatt av bokstaver fra utgangsalfabetet.
Apparatet for matematisk logikk, algebra, sannsynlighetsteori, kombinatorikk og grafteori er mye brukt.
Problemet med teorien om automater i noen av delene (strukturell teori om automater) vokste fra teorien om relé-kontaktkretser, som begynte å ta form på slutten av 1930-tallet. inklusive metoder for logisk algebra.

I den strukturelle teorien om automater studeres forskjellige typer skjemaer, designet for å beskrive hvordan en kompleks automat lages av enklere komponenter (elementer) riktig koblet i et system.
En annen retning, kalt den abstrakte teorien om automater, studerer oppførselen til automater (det vil si arten av transformasjonen av informasjon utført av dem), mens de abstraherer fra detaljene i deres interne struktur, og oppsto på 1950-tallet.
Innenfor rammen av den abstrakte teorien om automater er innholdet i begrepene "automat" og "maskin" i det vesentlige uttømt av standardbeskrivelsen av transformasjonen av informasjon som utføres av en automat. En slik transformasjon kan være deterministisk, men den kan også ha en sannsynlighet.
De mest studerte er deterministiske maskiner (automater), som inkluderer endelige automater - hovedobjektet for studiet i teorien om automater.
En endelig tilstandsmaskin er preget av en begrenset mengde minne (antall interne tilstander) og er definert ved hjelp av en overgangsfunksjon.Med en viss rimelig idealisering kan alle moderne matematiske maskiner og til og med hjernen, sett fra deres funksjonssynspunkt, betraktes som endelige automater.
Begrepene "sekvensiell maskin", "Milly-automat", "Moore-automat" brukes i litteraturen (og ikke ensartet av alle forfattere) som synonymer til begrepet "endelig automat" eller for å understreke visse funksjoner i overgangsfunksjonene til en endelig. automat.
Automata med ubegrenset minne er en Turing-maskin som er i stand til å utføre (potensielt) enhver effektiv informasjonstransformasjon. Konseptet "Turing-maskin" oppsto tidligere enn begrepet "finite state machine" og er hovedsakelig studert i teorien om algoritmer.
Abstrakt automatteori er nært beslektet med kjente algebraiske teorier, for eksempel semigruppeteori. Fra et anvendt synspunkt er resultatene som karakteriserer transformasjonen av informasjon i en automat når det gjelder minnestørrelse av interesse.
Dette er for eksempel tilfellet i problemer med eksperimenter på automater (verk av E.F. Moore, etc.), der en eller annen informasjon om overgangsfunksjonene til automaten eller om kapasiteten til dens minne hentes fra resultatene av eksperimenter.
En annen oppgave er å beregne periodene til utgangssekvensene, basert på tilgjengelig informasjon om minnestørrelsen til automaten og periodene til inngangssekvensene.
Av stor betydning er utviklingen av metoder for å minimere minnet til endelige tilstandsmaskiner og studere deres oppførsel i tilfeldige miljøer.
I abstrakt automatteori er synteseproblemet følgende.Når det gjelder et tydelig formalisert språk, er betingelsene skrevet for oppførselen til den utformede automaten (for hendelsen representert i automaten). I dette tilfellet er det nødvendig å utvikle metoder som i henhold til hver skriftlig tilstand:
1) finne ut om det eksisterer en slik tilstandsmaskin at informasjonen transformert av den oppfyller denne betingelsen;
2) hvis ja, blir overgangsfunksjonene til en slik begrenset tilstandsmaskin konstruert eller dens minnestørrelse estimert.
Løsningen av synteseoppgaven i en slik formulering forutsetter den foreløpige opprettelsen av et praktisk språk for å registrere driftsforholdene til en automat med praktiske algoritmer for overgangen fra opptak til transitive funksjoner.
I strukturteorien om automater består synteseproblemet i å konstruere en kjede av elementer av en gitt type som realiserer en begrenset automat gitt av dens overgangsfunksjoner. I dette tilfellet oppgir de vanligvis et optimalitetskriterium (for eksempel minimum antall elementer) og søker å oppnå et optimalt opplegg.
Som det viste seg senere, betyr dette at noen av metodene og konseptene som er utviklet tidligere i forhold til relé-kontaktkretser, er anvendelige for kretser av en annen type.
I forbindelse med utviklingen av elektroniske teknologier er ordningene mest utbredt av funksjonelle elementer (logiske nettverk). Et spesielt tilfelle av logiske nettverk er abstrakte nevrale nettverk, hvis elementer kalles nevroner.
Mange syntesemetoder er utviklet, avhengig av typen kretser og transformasjonen av informasjon de er ment for (Syntese av reléenheter).
Se -Minimering av kombinasjonskretser, Carnot-kart, kretssyntese
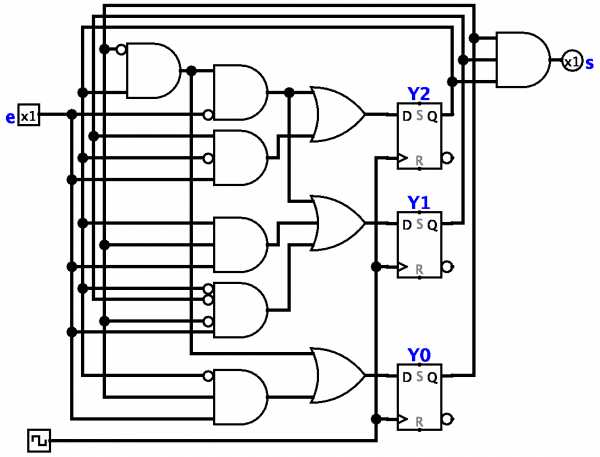
Finite state maskin — en matematisk modell av et kontrollsystem med en fast (ikke i stand til å øke under drift) minnestørrelse.
Konseptet med en endelig tilstandsmaskin er en matematisk abstraksjon som karakteriserer de generelle egenskapene til et sett med kontrollsystemer (for eksempel en multi-loop reléenhet). Alle slike systemer har fellestrekk som er naturlig å akseptere som definisjonen på en endelig automat.
Hver fullført automat har en inngang utsatt for ytre påvirkninger og indre elementer. For både input og interne elementer er det et fast antall diskrete tilstander de kan ta.
Endringen i tilstandene til inngangselementene og de interne elementene skjer ved diskrete øyeblikk i tid, intervallene mellom disse kalles tikker. Den interne tilstanden (tilstanden til det indre) på slutten av båndet bestemmes helt av den interne tilstanden og tilstanden til inngangen på begynnelsen av båndet.
Alle andre definisjoner av en endelig automat kan reduseres til denne karakteristikken, spesielt definisjoner som antar at en endelig automat har en utgang som avhenger av den interne tilstanden til automaten på et gitt tidspunkt.
Når det gjelder en slik karakteristikk, er arten av dens innganger og interne tilstander irrelevant for beskrivelsen av en komplett automat. I stedet for inndata og tilstander, kan du bare se på tallene deres i en tilfeldig nummerering.
Tilstandsmaskinen vil bli innstilt hvis avhengigheten av dens interne tilstandsnummer på det forrige interne tilstandsnummeret og det forrige inngangstilstandsnummeret er spesifisert. En slik oppgave kan være i form av et finalebord.
En annen vanlig måte å definere en komplett automat er konstruksjonen av den såkalte overgangsdiagrammer. Inndatatilstander kalles ofte bare innganger, og interne tilstander er ganske enkelt tilstander.
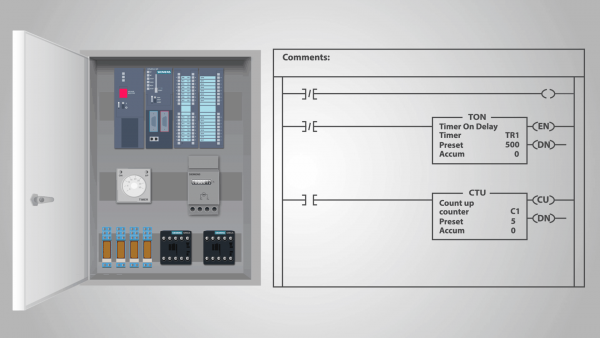
En endelig tilstandsmaskin kan være en modell av både tekniske enheter og noen biologiske systemer. Automater av den første typen er for eksempel reléenheter og ulike elektroniske datamaskiner, inkl. programmerbare logiske kontrollere.
Når det gjelder en reléenhet, spilles rollen til inngangstilstander av kombinasjoner av tilstander til de sensitive elementene i reléenheten (hver kombinasjon av slike tilstander er en «kompleks tilstand», karakterisert ved en indikasjon på alle de sensitive elementene i disse diskrete tilstandene som de har i et gitt øyeblikk). På samme måte fungerer kombinasjoner av tilstander av mellomelementer i en reléenhet som interne tilstander.
En programmerbar logisk kontroller (PLC) er et eksempel på en reléhandlingsenhet som kan kalles en frittstående tilstandsmaskin.
Faktisk, når programmet er lagt inn i PLS-en og kontrolleren har begynt å beregne, blir det ikke utsatt for ytre påvirkninger, og hver påfølgende tilstand er fullstendig bestemt av dens tidligere tilstand. Vi kan anta at inngangen har samme tilstand i hver klokkesyklus.
Motsatt kalles enhver endelig tilstandsmaskin som har den eneste mulige inngangstilstanden naturlig autonom, siden i dette tilfellet har det ytre miljøet ingen informasjon som kontrollerer dets oppførsel.
Se også:
Bruk av mikroprosessorsystemer i elektroteknikk på eksempel på bruk av PLS