Beregning av potensiometer og sammensatt shunt

Begreper og formler

Et potensiometer er en variabel motstand med en glider som er inkludert som vist i fig.

For flere detaljer se - Potensiometre og deres applikasjoner

En spenning U påføres punktene 1 og 2. En justerbar spenning fjernes fra punktene 2 og 3, hvis verdi er mindre enn U og avhenger av posisjonen til glideren. Spenningsdelere har et lignende opplegg, men de er ikke justerbare og har ikke en bevegelig glidebryter.

Potensiometre, spenningsdelere og komplekse shunter beregnes vha Kirchhoffs lover, for eksempel beregning av konvensjonelle kretser med motstander.

Eksempler av

1. Kildespenningen er U = 24 V, potensiometerets totale motstand er r = 300 Ohm. Motoren monteres separat slik at r1 = 50 ohm. Hvilken spenning U1 kan fjernes fra punkt 3 og 2 (fig. 1)?

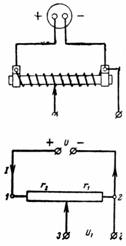
Ris. 1.

Strømmen I og spenningen U over motstanden r er relatert med formelen I ∙ r = U.

Potensiometerglideren skiller noe av motstanden, dvs. motstanden r1. Spenningsfallet mellom punkt 3 og 2 er lik I ∙ r1 = U1.

Fra forholdet mellom spenningsfallet får vi likheten (I ∙ r1) / (I ∙ r) = U1 / U. Jo større motstand r1, desto større er verdien av spenningen U1 mellom punktene 3 og 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. Potensiometeret (fig. 2) er lastet på en lampe med motstand r = 100 Ohm. Potensiometeret er delt med en glidebryter i to deler med r1 = 600 Ohm og r2 = 200 Ohm. Bestem spenningen Ul og lampestrømmen Il.

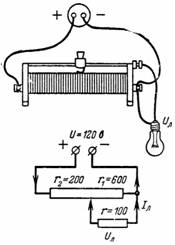
Ris. 2.

Strøm I går gjennom motstand r2 og strøm Il går gjennom lampen. En strøm I-Il flyter gjennom motstanden r1, som skaper en spenning over motstanden r1 lik lampespenningen: (I-Il) ∙ r1 = Ul.

På den annen side er lampespenningen lik kildespenningen minus spenningsfall ved motstand r2: U-I ∙ r2 = Ul.

Strømmen I er lik kildespenningen delt på den resulterende motstanden til den serie-parallelle forbindelsen til motstandene:

I = U / (r2 + (r ∙ r1) / (r + r1)).

Vi erstatter uttrykket for den totale strømmen til kilden i den andre ligningen:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Etter transformasjonen får vi et uttrykk for lampespenningen:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Hvis vi transformerer dette uttrykket, med utgangspunkt i at Ul = Il ∙ r, får vi et uttrykk for lampestrømmen:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Bytt ut de numeriske verdiene i de resulterende ligningene:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul/r = 36/100 = 0,36 A.

3. Beregn spenningen Opp og strømmen Ip til måleapparatet som er koblet til en del av potensiometeret. Enheten har en motstand på r = 1000 Ohm. Forgreningspunktet deler motstanden til deleren i r2 = 500 ohm og r1 = 7000 ohm (fig. 3).Spenning ved terminalene til potensiometeret U = 220 V.

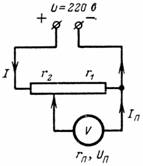
Ris. 3.

Ved å bruke formlene oppnådd tidligere kan vi skrive at strømmen som strømmer gjennom enheten er:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙00 = 010 500 = 010 500) 1,54 / 11 = 0,14 A.

Opp = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Beregn spenningen til enheten Up, hvis den bruker en strøm Ip = 20 mA og er koblet til et potensiometer delt inn i motstandene r2 = 10 ^ 4 Ohm og r1 = 2 ∙ 10 ^ 4 Ohm (fig. 3).

Den totale spenningen i spenningsdeleren er lik summen av spenningsfallene i dens deler (gjennom motstandene r1 og r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Opp

Kildestrømmen er forgrenet ved motorens kontaktpunkt: I = I1 + Ip; I = Upn / r1 + In.

Vi erstatter verdien av strømmen I i spenningsligningen:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Derfor er enhetens spenning Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Bytt ut de numeriske verdiene: Opp = (220-0,02 ∙ 10 000) / 30 000 ∙ 20 000 = 20/3 ∙ 2 = 13,3 V.

5. En likestrømskilde med spenning U = 120 V forsyner anodekretsene til radiomottakeren gjennom et potensiometer (spenningsdeler), som sammen med filteret har en motstand på r = 10000 Ohm. Spenningen U1 fjernes av motstanden r2 = 8000 Ohm. Beregn anodespenningen ved tomgang og ved laststrøm I = 0,02 A (fig. 4).

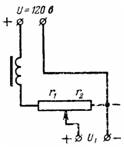
Ris. 4.

Det første tilfellet ligner på eksempel 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Det andre tilfellet ligner på eksempel 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Ved lading vil spenningen falle fra 96 ​​til 64 V.Hvis det er behov for mer spenning, skal glideren flyttes til venstre, det vil si at motstanden r2 skal økes.

6. Spenningene Ua og Ub fjernes av spenningsdeleren. Den totale motstanden til spenningsdeleren koblet til spenningen U1 = 220 V er r = 20 000 Ohm. Hva er spenningen Ua i motstanden r3 = 12000 Ohm med strømforbruk Ia = 0,01 A og spenningen Ub i motstanden r2 + r3 = 18000 Ohm med strømforbruk Ib = 0,02 A (fig. 5).

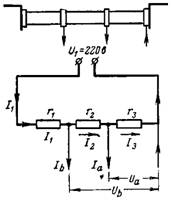
Ris. 5.

Spenningsmotstand r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

Spenningen Ub er lik summen av spenningsfallet Ua over motstanden r3 og spenningsfallet over motstanden r2. Spenningsfallet over motstand r2 er lik I2 ∙ r2. Strøm I2 = Ia + I3. Strømmen I3 kan beregnes som i eksempel 1:

I3 = (220-80-40) / 20 000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Spenning Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

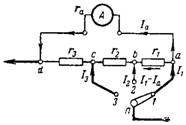
7. Beregn den kombinerte shunten for milliammeteret slik at den ved forskjellige posisjoner av bryteren har følgende måleområder: I1 = 10 mA; I2 = 30mA; I3 = 100mA. Shuntkoblingsskjemaet er vist i fig. 6. Intern motstand til enheten ra = 40 Ohm. Indre måleområde på milliammeter 2 mA.

Ris. 6.

Ved måling av strøm I≤2mA er shunten slått av.

a) Ved måling av strømmen I = 10 mA er bryteren i posisjon 1 og en strøm på 10-2 = 8 mA går gjennom alle shuntmotstandene. Spenningsfallet over shuntmotstanden Ush og enheten Ua mellom punktene d og a må være lik

Ush = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Ved måling av strøm I2 = 30 mA står bryteren i posisjon 2. Den målte strømmen vil dele seg i punkt b. Ved full avbøyning av enhetens peker vil strømmen Ia = 2 mA passere gjennom motstanden r1 og enheten ra.

Resten av strømmen I2-Ia vil gå gjennom motstandene r2 og r3. Strømmene vil skape det samme spenningsfallet over de to grenene mellom punktene d og b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) På lignende måte vil vi utføre beregningen når vi øker måleområdet til I3 = 100 mA. Strøm I3-Ia vil flyte gjennom motstand r3 og strøm Ia gjennom motstand r1, r2, ra. Spenningen i begge grenene er den samme: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Vi fikk tre likninger med tre ukjente verdier av motstandene r1, r2 og r3.

Vi multipliserer alle ligningene med 1000 og konverterer dem:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -rl = 40;

49 ∙ r3-r1-r2 = 40.

La oss legge til den første og tredje ligningen: 50 ∙ r3 = 50;

r3 = 50/50 = 1 ohm.

La oss legge til den første og andre ligningen: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 ohm.

La oss erstatte de oppnådde resultatene i den første ligningen: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 ohm.

Riktigheten av beregningen kan kontrolleres ved å erstatte de oppnådde motstandsverdiene i ligningene.