Spenningsfall

Begreper og formler

Ved hver motstand r, når strømmen I går, vises en spenning U = I ∙ r, som vanligvis kalles spenningsfallet til denne motstanden.

Hvis det kun er én motstand r i kretsen, faller hele kildespenningen Ust på denne motstanden.

Hvis kretsen har to motstander r1 og r2 koblet i serie, så er summen av spenningene i motstandene U1 = I ∙ r1 og U2 = I ∙ r2, dvs. spenningsfallet er lik kildespenningen: Ust = U1 + U2.

Forsyningsspenningen er lik summen av spenningsfallet i kretsen (Kirchhoffs 2. lov).

Eksempler av

1. Hvilket spenningsfall oppstår over glødetråden til lampen med motstand r = 15 Ohm når strømmen I = 0,3 A passerer (fig. 1)?

Ris. 1.

Antall spenningsfall Ohms lov: U = I ∙ r = 0,3 ∙ 15 = 4,5 V.

Spenningen mellom punkt 1 og 2 på lampen (se diagrammet) er 4,5 V. Lampen lyser normalt hvis merkestrømmen går gjennom den eller hvis det er merkespenning mellom punkt 1 og 2 (merkestrømmen og spenningen er angitt på lampen).

2. To identiske pærer for en spenning på 2,5 V og en strøm på 0,3 A kobles i serie og kobles til et lommebatteri med en spenning på 4,5 V. Hvilket spenningsfall genereres ved terminalene til de enkelte pærene (fig. 2) ) ) ?

Ris. 2.

Identiske pærer har samme motstand r. Når de er koblet i serie, går den samme strømmen I gjennom dem. Det følger at de vil ha samme spenningsfall, summen av disse spenningene må være lik kildespenningen U = 4,5 V. Hver pære har en spenning på 4 , 5:2 = 2,25V.

Du kan løse dette problemet og sekvensiell beregning. Vi beregner motstanden til pæren i henhold til dataene: rl = 2,5 / 0,3 = 8,33 Ohm.

Kretsstrøm I = U / (2rl) = 4,5 / 16,66 = 0,27 A.

Spenningsfallet over pæren U = Irl = 0,27 ∙ 8,33 = 2,25 V.

3. Spenningen mellom skinnen og kontaktledningen til trikkelinjen er 500 V. Fire identiske lamper koblet i serie brukes til belysning. For hvilken spenning skal hver lampe (fig. 3) velges?

Ris. 3.

Identiske lamper har like motstand som den samme strømmen flyter gjennom. Spenningsfallet over lampene vil også være det samme. Dette betyr at for hver lampe vil det være 500:4 = 125 V.

4. To lamper med en effekt på 40 og 60 W med en nominell spenning på 220 V er koblet i serie og er koblet til et nettverk med en spenning på 220 V. Hvilket spenningsfall oppstår over hver av dem (fig. 4)?

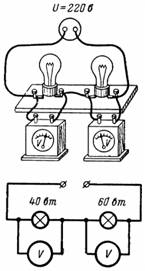
Ris. 4.

Den første lampen har en motstand r1 = 1210 Ohm, og den andre r2 = 806,6 Ohm (i oppvarmet tilstand). Strømmen som går gjennom lampene er I = U / (r1 + r2) = 220 / 2016,6 = 0,109 A.

Spenningsfall i den første lampen U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.

Spenningsfall i den andre lampen U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.

En lampe med høyere motstand har større spenningsfall og omvendt. Glødetrådene til begge lampene er veldig svake, men 40W-lampen er litt sterkere enn 60W-lampen.

5. For at spenningen til den elektriske motoren D (fig. 5) skal være lik 220 V, må spenningen i begynnelsen av den lange linjen (ved kraftverket) være mer enn 220 V i verdi spenningsfall (tap) på nett. Jo større motstanden til linjen og strømmen i den er, desto større er spenningsfallet langs linjen.

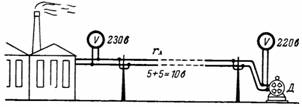Ris. 5.

I vårt eksempel er spenningsfallet i hver ledning på linjen 5 V. Da skal spenningen ved samleskinnene til kraftverket være lik 230 V.

6. Forbrukeren drives av et 80 V batteri med en strøm på 30 A. For normal drift av forbrukeren er 3 % spenningsfall i aluminiumsledninger med tverrsnitt 16 mm2 tillatt. Hva er maksimal avstand fra batteriet til brukeren?

Tillatt spenningsfall i ledningen U = 3/100 ∙ 80 = 2,4 V.

Motstanden til ledningene er begrenset av det tillatte spenningsfallet rpr = U / I = 2,4 / 30 = 0,08 Ohm.

Ved å bruke formelen for å bestemme motstanden, beregner vi lengden på ledningene: r = ρ ∙ l / S, hvorfra l = (r ∙ S) / ρ = (0,08 ∙ 16) / 0,029 = 44,1 m.

Hvis brukeren er 22 m fra batteriet, vil spenningen i det være mindre enn 80 V ved 3 %, dvs. lik 77,6 V.

7. En 20 km lang telegraflinje er laget av ståltråd med en diameter på 3,5 mm. Returledningen erstattes av jording gjennom metallskinner. Motstanden til overgangen mellom buss og jord er rz = 50 Ohm.Hva skal batterispenningen være i begynnelsen av linjen hvis motstanden til reléet på slutten av linjen er рп = 300 Ohm og reléstrømmen er I = 5 mA?

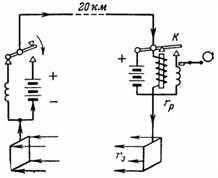
Ris. 6.

Koblingsskjemaet er vist i fig. 6. Når telegrafbryteren trykkes på punktet for sending av signalet, tiltrekker reléet ved mottakspunktet ved enden av linjen ankeret K, som igjen slår på spolen til opptakeren med sin kontakt. Utgangsspenningen må kompensere for spenningsfallet i linjen, mottaksreléet og transientmotstandene til jordingsskinnene: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rр; U = I ∙ (rр + рр + 2 ∙ rр).

Kildespenningen er lik produktet av strømmen og den totale motstanden til kretsen.

Trådtverrsnitt S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.

Linjemotstand rl = ρ ∙ l / S = 0,11 ∙ 20 000 / 9,6 = 229,2 ohm.

Resulterende motstand r = 229,2 + 300 + 2 ∙ 50 = 629,2 Ohm.

Utgangsspenning U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3,2 V.

Spenningsfallet i linjen under passering av en strøm I = 0,005 A vil være: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.

Det relativt lave spenningsfallet i ledningen oppnås på grunn av den lave verdien av strømmen (5 mA). Derfor må det ved mottakspunktet være et følsomt relé (forsterker), som slås på av en svak 5 mA-puls og gjennom kontakten slår på et annet, kraftigere relé.

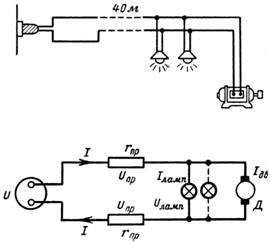
8. Hvor høy er spenningen til lampene i kretsen på fig. 28, når: a) motoren ikke er slått på; b) motoren starter; c) motoren går.

Motoren og 20 lamper er koblet til 110 V nettspenning. Lampene er konstruert for 110 V og 40 W. Startstrømmen til motoren er Ip = 50 A og dens merkestrøm er In = 30 A.

Den innførte kobbertråden har et tverrsnitt på 16 mm2 og en lengde på 40 m.

Fig. 7 og forholdene for problemet, kan det sees at motor- og lampestrømmen får linjespenningen til å falle, derfor vil belastningsspenningen være mindre enn 110V.

Ris. 7.

U = 2 ∙ Ul + Ulamp.

Derfor er spenningen på lampene Ulamp = U-2 ∙ Ul.

Det er nødvendig å bestemme spenningsfallet i linjen ved forskjellige strømmer: Ul = I ∙ rl.

Motstand av hele linjen

2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 Ohm.

Strømmen som går gjennom alle lampene

20 ∙ Ilamp = 20 ∙ 40/110 = 7,27 A.

Nettspenningsfall når bare lamper er på (ingen motor),

2 ∙ Ul = Ilamp ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.

Spenningen i lampene i dette tilfellet er:

Ulamp = U-2 ∙ Ul = 110-0,65 = 109,35 V.

Når du starter motoren, vil lampene lyse mer svakt, siden spenningsfallet i linjen er større:

2 ∙ Ul = (Ilamp + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.

Minimumsspenningen på lampene ved start av motoren vil være:

Ulamp = Uc-2, Ul = 110-5,1 = 104,9V.

Når motoren går, er spenningsfallet i ledningen mindre enn når motoren startes, men mer enn når motoren er av:

2 ∙ Ul = (Ilamp + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.

Spenningen til lampene under normal motordrift er:

Ulamp = 110-3,32 = 106,68 V.

Selv en liten reduksjon i spenningen til lampene i forhold til den nominelle påvirker lysstyrken på belysningen betydelig.