Beregning av den resulterende motstanden i serie-parallell forbindelse

Begreper og formler

En serie-parallell eller blandet forbindelse er en kompleks forbindelse av tre eller flere motstander. Den resulterende motstanden til en blandet forbindelse beregnes trinnvis ved hjelp av formler for beregning av motstand i serie- og parallellkoblinger.

Eksempler av

1. Beregn serie-parallellkoblingen av tre motstander i henhold til diagrammet i fig. 1.

Bytt først ut de parallellkoblede motstandene r2 og r3 med den resulterende motstanden r (2-3):

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 ohm.

Den resulterende motstanden til hele kretsen er r = r1 + r (2-3) = 5 + 6,6 = 11,6 ohm.

Ris. 1.

2. Hvilken strøm som går gjennom kretsen (fig. 2) i åpne og lukkede tilfeller knivbryter P? Hvordan endres spenningen over motstand r2 i begge tilfeller?

Ris. 2.

a) Bryteren er åpen. Resulterende motstand av seriekoblede motstander r1 og r2

r (1-2) = r1 + r2 = 25 ohm.

Strøm I (1-2) = U / r (1-2) = 100/25 = 4 A.

Spenningsfall over motstand r2

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

b) Bryteren er lukket. Resulterende motstand av motstandene r1 og r3 koblet parallelt

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 ohm.

Den totale motstanden til hele kretsen er r = r (1-3) + r2 = 6,6 + 5 = 11,6 ohm.

Strøm I = U / r = 100 / 11,6 = 8,62 A.

Spenningsfallet over motstanden r2 er i dette tilfellet lik: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

I det andre tilfellet økte strømmen som et resultat av å koble den parallelle motstanden R3. Mer aktuell skaper mer spenningsfall ved motstand r2.

3. Hva bør være ekstra motstand rd, slik at to lamper koblet parallelt for en spenning på 120 V og en strøm på 0,2 A kan kobles til et nettverk med en spenning på U = 220 V (fig. 3)?

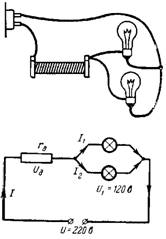
Ris. 3.

Spenningen i lampene skal være lik 120 V. Den gjenværende spenningen (100 V) faller på den ekstra motstanden rd. En strøm av to lamper I = 0,4 A flyter gjennom motstanden rd.

I følge Ohms lov rd = Ud / I = 100 / 0,4 = 250 Ohm.

4. Elektroniske lamper med en 1,2 V glødetråd og en glødetrådsstrøm på 0,025 og 0,05 A er koblet i serie til en DC-kilde med spenning 4,5 V. Hva skal være den ekstra motstanden rd og parallell motstand (shunt) til en lampe med lavere glødestrøm (fig. 4)?

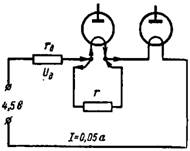
Ris. 4.

Motstandene i kretsen må velges slik at glødestrømmen til den andre lampen flyter I = 0,05 A. Spenningen over glødetråden til de elektroniske lampene vil være 1,2 + 1,2 = 2,4 V. Trekker vi denne verdien fra batterispenningen, vi ta verdien av spenningsfallet over den ekstra motstanden rd: Ud = 4,5-2,4 = 2,1 V.

Derfor er den ekstra motstanden rd = (Ud) / I = 2,1 / 0,05 = 42 Ohm.

En filamentstrøm på 0,05 A skal ikke strømme gjennom filamentet til det første vakuumrøret. Halvparten av denne strømmen (0,05-0,025 = 0,025 A) må passere gjennom shunten r. Shuntspenningen er den samme som glødetråden til lampen, dvs. 1,2 V. Derfor er shuntmotstanden: r = 1,2 / 0,025 = 48 Ohm.

5. Hva er den resulterende kretsmotstanden og strømmen i den i kretsen på fig. 5?

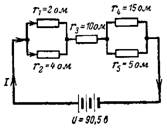
Ris. 5.

La oss først bestemme den resulterende motstanden til de parallellkoblede motstandene:

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 ohm;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 ohm.

Den resulterende kretsmotstanden er:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 ohm.

Den resulterende strømmen ved spenning U = 90,5 V

I = U / r = 90,5 / 15,05 = 6 A.

6. Beregn den resulterende motstanden til en kompleks serie-parallell forbindelse i kretsen på fig. 6. Beregn den resulterende strømmen I, strømmen I4 og spenningsfallet over motstanden r1.

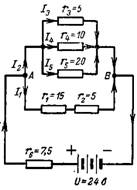
Ris. 6.

Resulterende konduktans av parallellkoblede motstander

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 ohm.

Kretsmotstanden til r1 og r2 er:

r (1-2) = r1 + r2 = 15 + 5 = 20 ohm.

Den resulterende ledningsevnen og motstanden mellom punktene A og B er henholdsvis lik: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 ohm.

Den resulterende motstanden til hele kretsen er r = rAB + r6 = 2,5 + 7,5 = 10 ohm.

Den resulterende strømmen er I = U / r = 24/10 = 2,4 A.

Spenningen mellom punktene A og B er lik kildespenningen U minus spenningsfallet over motstanden r6

UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.

Motstanden r4 er koblet til denne spenningen, så strømmen gjennom den vil være lik:

I4 = UAB / r4 = 6/10 = 0,6A.

Motstander r1 og r2 har et felles spenningsfall UAB, så strømmen gjennom r1 er:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Spenningsfall over motstand r1

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

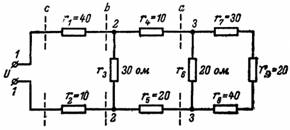
7. Hva er den resulterende motstanden og strømmen i kretsen på fig. 7 hvis kildespenningen er U = 220 V?

Ris. 7.

Vi starter med kretsen som ligger til høyre for nodene 3 og 3. Motstandene r7, r8, r9 er koblet i serie, derfor

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 ohm.

En motstand r6 er koblet parallelt med denne motstanden, så den resulterende motstanden ved node 3 og 3 (seksjon a)

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 ohm.

Motstander r4 og r5 er koblet i serie med motstand ra:

r (4-5-a) = 10 + 20 + 16,36 = 46,36 ohm.

Resulterende motstand av node 2 og 2 (seksjon b)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 ohm.

Den resulterende motstanden til hele kretsen er r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 ohm.

Den resulterende strømmen er I = U / r = 220 / 68,28 = 3,8 A.