Beregning av kondensatorkapasitans

Kapasitans C er kapasiteten til kondensatoren til å akseptere (lagre og holde) mengden elektrisitet Q i ampere-sekunder eller ladningen Q i pendanter. Hvis du forteller et legeme, for eksempel en ball, en elektrisk ladning (elektrisitetsmengde) Q, så vil et elektroskop koblet mellom denne kroppen og bakken vise en spenning U (fig. 1). Denne spenningen er proporsjonal med ladningen og avhenger også av formen og størrelsen på kroppen.

Forholdet mellom ladning Q og spenning U uttrykkes med formelen Q = C ∙ U.

Proporsjonalitetskonstanten C kalles kroppens kapasitans. Hvis kroppen har form som en kule, er kapasitansen til kroppen proporsjonal med radien til kulen r.

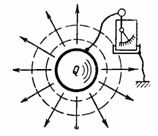
Ris. 1.

Måleenheten for kapasitans er farad (F).

Kroppen har en kapasitans på 1 F når en ladning på 1 k produserer en spenning på 1 V. mellom den og bakken. Farads er en veldig stor måleenhet, så mindre enheter brukes i praksis: mikrofarad (μF), nanofarad (nF) og picofarad (pF)...

Disse enhetene er relatert med følgende forhold: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Kapasitansen til en ball med en radius på 1 cm er 1,1 pF.

Ikke bare en isolert kropp kan akkumulere ladning, men også en spesiell enhet kalt en kondensator. En kondensator består av to eller flere plater (plater) som er adskilt av et dielektrikum (isolasjon).

I fig. 2 viser en krets med en likestrømskilde koblet til en kondensator. Når den er slått på, dannes en positiv ladning +Q i den høyre platen på kondensatoren og en negativ ladning -Q i den venstre platen. I løpet av kondensatorlading en strøm flyter gjennom kretsen, som stopper etter slutten av ladingen; da vil spenningen over kondensatoren være lik e. etc. c. kilde U. Ladningen på kondensatorplaten, spenning og kapasitans er relatert til forholdet Q = C ∙ U. I dette tilfellet dannes det et elektrostatisk felt i kondensatorens dielektrikum.

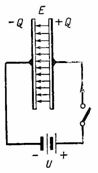
Ris. 2.

Kapasiteten til en kondensator med et luftdielektrisk kan beregnes med formelen C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, hvor S er arealet til en plate, cm2; d er avstanden mellom platene, cm; C er kapasitansen til kondensatoren, pF.

Kapasiteten til en kondensator som består av n plater (fig. 3) er lik: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

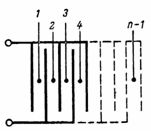
Ris. 3.

Hvis rommet mellom platene er fylt med et annet dielektrikum, for eksempel papir, vil kapasitansen til kondensatoren øke med en faktor på ε. Når papirisolasjon brukes, vil kapasiteten øke 3 ganger, med glimmerisolasjon - 5-8 ganger, med glass - 7 ganger, etc. Verdien av ε kalles dielektrikumets dielektriske konstant.

Den generelle formelen for å bestemme kapasitansen til en kondensator med dielektrisk konstant ε (epsilon) er: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Denne formelen er nyttig for å beregne små variable kondensatorer for radioer.Den samme formelen kan representeres som: C = (ε_0 ∙ ε ∙ S) / d, hvor ε_0 er den dielektriske konstanten eller den dielektriske konstanten til vakuumet (ε_0 = 8.859 ∙ 10 ^ (- 12) F / m); ε er dielektrikumets dielektriske konstant.

I denne formelen erstattes dimensjonene i meter, og kapasitansen oppnås i farad.

Eksempler av

1. Hva er kapasiteten til planeten Jorden, hvis radius er r = 6378 km?

Siden kapasitansen til en kule med en radius på 1 cm er lik 1,11 pF, er kapasitansen til jorden: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Kapasiteten til en ball på størrelse med planeten vår er relativt liten. Små elektrolytiske kondensatorer har denne kapasiteten).

2. Bestem kapasitansen til en kondensator som består av to plater som hver har et areal S = 120 cm2.

Platene er atskilt med et luftlag med en tykkelse på d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Bestem kapasitansen til kondensatoren med dataene gitt i forrige eksempel, hvis rommet mellom platene er fylt med vokspapir med en dielektrisk konstant ε = 4, glass (ε = 7), elektrisk papp (ε = 2) glimmer (e = 8).

En vokspapirkondensator har en kapasitans C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Kapasitansen til en glasskondensator er C = 7 ∙ 21,2 = 148,4 pF.

Kapasitansen til pappkondensatoren er C = 2 ∙ 21,2 = 42,3 pF.

Kapasitansen til glimmerkondensatoren er C = 8 ∙ 21,2 = 169,6 pF.

4. Hva er kapasitansen til en luftroterende kondensator for en radiomottaker som består av 20 plater med et areal på 20 cm2 hvis avstanden mellom platene er 0,06 cm (fig. 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondensatoren vist i fig.3, består av separate enkleste kondensatorer med to plater, hvis antall er lik n-1.

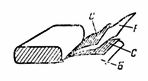
5. En papirkondensator med kapasitans C = 2 μF består av to strimler av stanniol C og to strimler av et dielektrikum laget av vokspapir B med en dielektrisk konstant ε = 6. Tykkelsen på vokspapiret er d = 0,1 mm. De brettede stripene rulles sammen, ledningene er laget av stålplatene. Bestem lengden på kondensatorstålstrimmelen hvis bredden er 4 cm (fig. 4).

Ris. 4.

Først bestemmer vi arealet til en stripe med formelen C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, hvorav S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Lengden på hver stripe er l = 37680/4 = 9420 cm = 94,2 m.