Lading og utlading av kondensatoren

Kondensatorlading

For å lade kondensatoren må du koble den til DC-kretsen. I fig. 1 viser kondensatorladekretsen. Kondensator C er koblet til terminalene på generatoren. Nøkkelen kan brukes til å lukke eller åpne kretsen. La oss ta en detaljert titt på prosessen med å lade en kondensator.

Generatoren har indre motstand. Når bryteren er lukket, vil kondensatoren lades til en spenning mellom platene lik f.eks. etc. v. generator: Uc = E. I dette tilfellet mottar platen koblet til den positive terminalen til generatoren en positiv ladning (+q), og den andre platen mottar en lik negativ ladning (-q). Størrelsen på ladningen q er direkte proporsjonal med kapasiteten til kondensatoren C og spenningen på platene: q = CUc

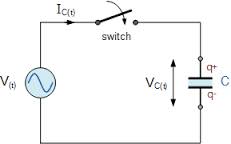
Pe. 1... Kondensatorladekrets

For å lade kondensatorplatene er det nødvendig at en av dem får og den andre mister en viss mengde elektroner.Overføringen av elektroner fra en plate til en annen utføres langs den eksterne kretsen av den elektromotoriske kraften til generatoren, og prosessen med å flytte ladninger langs kretsen er ikke annet enn en elektrisk strøm, kalt en ladekapasitiv strøm A ladning

Ladestrømmen i verdi flyter vanligvis i tusendeler av et sekund til spenningen over kondensatoren når en verdi lik e. etc. v. generator. Grafen over spenningsøkningen på kondensatorplatene under ladingen er vist i fig. 2, a, hvorfra det kan sees at spenningen Uc øker jevnt, først raskt, og så langsommere og langsommere, inntil den blir lik f.eks. etc. v. generator E. Etter det forblir spenningen over kondensatoren uendret.

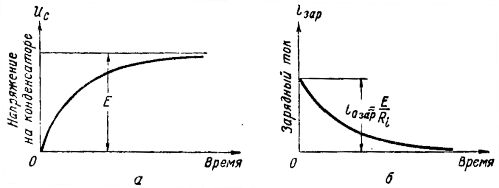
Ris. 2. Grafer over spenning og strøm ved lading av en kondensator

Når kondensatoren lades, flyter en ladestrøm gjennom kretsen. Ladestrømgrafen er vist i fig. 2, b. I det første øyeblikket har ladestrømmen den største verdien, siden spenningen i kondensatoren fortsatt er null, og ifølge Ohms lov iotax = E /Ri, siden alle e., etc. c generator påføres motstand Ri.

Når kondensatoren lades, det vil si øker spenningen over den, synker den for ladestrømmen. Når det allerede er en spenning over kondensatoren, vil spenningsfallet over motstanden være lik forskjellen mellom f.eks. etc. v. generator- og kondensatorspenning, dvs. lik E — U s. Derfor itax = (E-Us) / Ri

Herfra kan man se at når Uc øker, ilader og ved Uc = E blir ladestrømmen null.

Les mer om Ohms lov her: Ohms lov for en del av en krets

Varigheten av kondensatorladeprosessen avhenger av to mengder:

1) fra den indre motstanden til generatoren Ri,

2) fra kapasitansen til kondensatoren C.

I fig. 2 viser grafene for de elegante strømmene for en kondensator med en kapasitet på 10 mikrofarad: kurve 1 tilsvarer ladeprosessen fra en generator med f.eks. etc. med E = 100 V og med en indre motstand Ri= 10 Ohm, tilsvarer kurve 2 ladeprosessen fra en generator med samme e. pr. med, men med lavere indre motstand: Ri = 5 ohm.

Fra en sammenligning av disse kurvene kan det ses at med en lavere indre motstand i generatoren, er styrken til den elegante strømmen i det første øyeblikket større og derfor er ladeprosessen raskere.

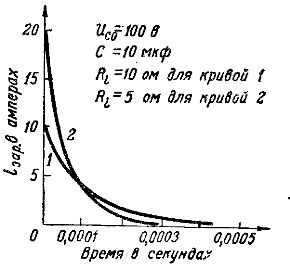
Ris. 2. Grafer over ladestrømmer ved forskjellige motstander

I fig. 3 sammenligner grafene for ladestrømmer ved lading fra samme generator med f.eks. etc. med E = 100 V og intern motstand Ri= 10 ohm av to kondensatorer med forskjellig kapasitet: 10 mikrofarad (kurve 1) og 20 mikrofarad (kurve 2).

Startladestrøm iotax = E /Ri = 100/10 = 10 Begge kondensatorene er de samme, siden en kondensator med større kapasitet lagrer mer elektrisitet, bør ladestrømmen ta lengre tid, og ladeprosessen er mer - lang.

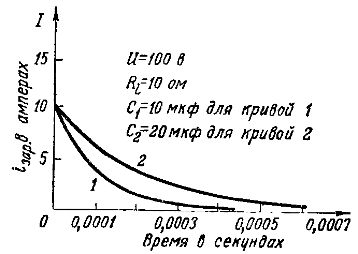
Ris. 3. Tabeller over ladestrømmer med ulik kapasitet

Kondensatorutladning

Koble den ladede kondensatoren fra generatoren og fest en motstand til platene.

Det er en spenning på platene til kondensatoren Us, derfor, i en lukket krets, vil en strøm som kalles utladningskapasitive strøm ires flyte.

Strøm flyter fra den positive platen til kondensatoren gjennom motstanden til den negative platen. Dette tilsvarer overgangen av overflødige elektroner fra den negative platen til den positive, hvor de er fraværende.Prosessen med radrammer foregår til potensialene til de to platene er like, det vil si at potensialforskjellen mellom dem blir null: Uc = 0.

I fig. 4a viser grafen for reduksjonen av spenningen i kondensatoren under utlading fra verdien Uco = 100 V til null, og spenningen synker først raskt, og deretter langsommere.

I fig. 4, b viser grafen for endringene i utladningsstrømmen. Styrken på utladningsstrømmen avhenger av verdien av motstanden R og i henhold til Ohms lov ires = Uc/R

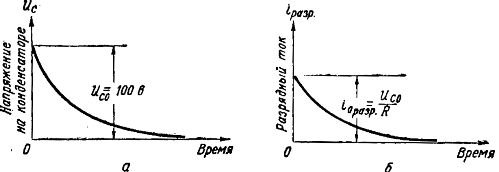
Ris. 4. Grafer over spenning og strømmer under kondensatorutladning

I det første øyeblikket, når spenningen på platene til kondensatoren er størst, er utladningsstrømmen også størst, og med en reduksjon i Uc under utladningen avtar også utladningsstrømmen. Ved Uc = 0 stopper utladningsstrømmen.

Varigheten av avhendingen avhenger av:

1) fra kapasitansen til kondensatoren C

2) på verdien av motstanden R som kondensatoren utlades til.

Jo større motstand R, jo langsommere vil utladningen skje. Dette skyldes det faktum at med stor motstand er styrken på utladningsstrømmen liten og mengden ladning på kondensatorplatene avtar sakte.

Dette kan vises i grafene for utladningsstrømmen til den samme kondensatoren, med en kapasitet på 10 μF og ladet til en spenning på 100 V, ved to forskjellige motstandsverdier (fig. 5): kurve 1 - ved R =40 ohm, ioresr = UcО/ R = 100/40 = 2,5 A og kurve 2 — ved 20 Ohm ioresr = 100/20 = 5 A.

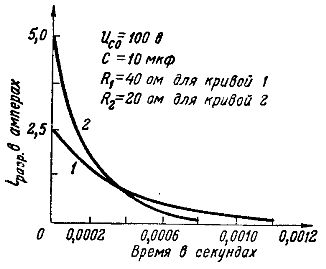
Ris. 5. Grafer over utladningsstrømmene ved forskjellige motstander

Utladningen er også langsommere når kapasitansen til kondensatoren er stor.Dette er fordi med mer kapasitans på kondensatorplatene blir det mer elektrisitet (mer ladning) og det vil ta lengre tid før ladningen tappes. Dette er tydelig vist av grafene for utladningsstrømmene for to kondensatorer med samme kapasitet, ladet til samme spenning på 100 V og utladet til en motstand R= 40 ohm (fig. 6: kurve 1 — for en kondensator med kapasitet på 10 mikrofarad og kurve 2 — for kondensator med en kapasitet på 20 mikrofarad).

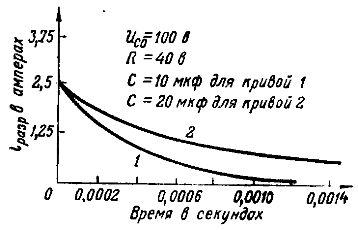
Ris. 6. Grafer over utladningsstrømmene ved forskjellige styrker

Fra de vurderte prosessene kan det konkluderes med at i en krets med en kondensator flyter strømmen bare i øyeblikkene for lading og utlading, når spenningen på platene endres.

Dette forklares av det faktum at når spenningen endres, endres ladningsmengden på platene, og dette krever bevegelse av ladninger langs kretsen, det vil si at en elektrisk strøm må passere gjennom kretsen. En ladet kondensator passerer ikke likestrøm fordi dielektrikumet mellom platene åpner kretsen.

Kondensator energi

Under ladeprosessen lagrer kondensatoren energi ved å motta den fra generatoren. Når en kondensator utlades, omdannes all energien til det elektriske feltet til varmeenergi, det vil si at den går til å varme opp motstanden som kondensatoren utlades gjennom. Jo større kapasitansen til kondensatoren og spenningen over platene er, jo større er energien til kondensatorens elektriske felt. Mengden energi som besittes av en kondensator med kapasitet C ladet til en spenning U er lik: W = Wc = CU2/2

Et eksempel. Kondensator C = 10 μF ladet til spenning Uc = 500 V.Bestem energien som vil bli frigjort i varmekraften ved motstanden som kondensatoren utlades gjennom.

Svar. Under utlading vil all energien som er lagret av kondensatoren omdannes til varme. Derfor W = Wc = CU2/2 = (10 x 10-6 x 500) / 2 = 1,25 J.