Beregning av varmeelementet

For å bestemme en av hovedparametrene til ledningen til varmeelementet - diameter d, m (mm), brukes to beregningsmetoder: i henhold til den tillatte spesifikke overflateeffekten PF og ved å bruke tabellen over strømbelastninger.

Tillatt spesifikk overflateeffekt PF= P⁄F,

hvor P er kraften til trådvarmeren, W;

F = π ∙ d ∙ l — varmeapparatareal, m2; l — trådlengde, m.

I henhold til den første metoden

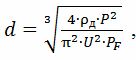
hvor ρd — elektrisk motstand til trådmaterialet ved faktisk temperatur, Ohm • m; U er varmetrådspenningen, V; PF — tillatte verdier for spesifikk overflateeffekt for forskjellige varmeovner:

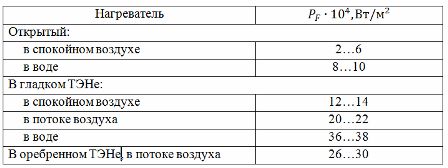
Den andre metoden bruker en tabell over strømbelastninger (se tabell 1) satt sammen fra eksperimentelle data. For å bruke den angitte tabellen, er det nødvendig å bestemme den beregnede oppvarmingstemperaturen Tp relatert til den faktiske (eller tillatte) temperaturen til lederen Td ved forholdet:

Tr = Km ∙ Ks ∙ Td,

hvor Km er installasjonsfaktoren, tatt i betraktning forringelsen av kjøleforholdene til varmeren på grunn av dens konstruksjon; Kc er omgivelsesfaktoren, med tanke på forbedringen av varmerens kjøleforhold sammenlignet med et stasjonært luftmiljø.

For et varmeelement laget av tråd vridd i en spiral, Km = 0,8 … 0,9; det samme, med en keramisk base Km = 0,6 ... 0,7; for en ledning av varmeplater og noen varmeelementer Km = 0,5 ... 0,6; for en leder fra et elektrisk gulv, jord og varmeelementer Km = 0,3 ... 0,4. En mindre verdi på Km tilsvarer en varmeovn med mindre diameter, en større verdi til en større diameter.

Ved drift under andre forhold enn fri konveksjon, tas Kc = 1,3 … 2,0 for varmeelementer i luftstrømmen; for elementer i stille vann Kc = 2,5; i vannføringen — Kc = 3,0 … 3,5.

Hvis spenningen Uph og kraften Pf for fremtidens (designede) varmeapparat er innstilt, er dens strøm (per fase)

Iph = Pph⁄Uph

I henhold til den beregnede verdien av strømmen til varmeren for den nødvendige beregnede temperaturen for oppvarmingen i henhold til tabell 1, er den nødvendige diameteren til nikromtråden d funnet og den nødvendige lengden på ledningen, m, for fremstilling av varmeren er beregnet:

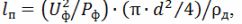
hvor d er den valgte tråddiameteren, m; ρd er den spesifikke elektriske motstanden til lederen ved den faktiske oppvarmingstemperaturen, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

hvor αр — temperaturkoeffisient for motstand, 1/OS.

For å bestemme parametrene til nikromspiralen, ta gjennomsnittsdiameteren til svingene D = (6 … 10) ∙ d, spiralens stigning h = (2 … 4) ∙ d,

antall svinger

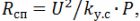
helixlengde lsp = h ∙ n.

Når du beregner varmeelementene, bør det huskes at motstanden til spiraltråden etter å ha trykket på varmeelementet

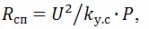
hvor k (y.s) er en koeffisient som tar hensyn til reduksjonen i motstanden til spiralen; i henhold til eksperimentelle data, k (s) = 1,25. Det bør også tas i betraktning at den spesifikke overflateeffekten til spiraltråden er 3,5 ... 5 ganger større enn den spesifikke overflateeffekten til det rørformede varmeelementet.

I praktiske beregninger av varmeelementet, bestemme først temperaturen på overflaten Tp = To + P ∙ Rt1,

hvor det er omgivelsestemperaturen, ° C; P er kraften til varmeelementet, W; RT1 — termisk motstand ved røret — medium grensesnitt, ОC / W.

Deretter bestemmes temperaturen på viklingen: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

hvor Rt2 er den termiske motstanden til rørveggen, ОC / W; RT3 — termisk motstand av fyllstoffet, ОC / W; Rp1 = 1⁄ (α ∙ F), hvor α er varmeoverføringskoeffisienten, W / (m ^ 2 • ОС); F - området til varmeren, m2; Rt2 = δ⁄ (λ ∙ F), hvor δ er veggtykkelsen, m; λ — termisk ledningsevne av veggen, W / (m • ОС).

For mer informasjon om enheten til varmeelementene, se her: Varmeelementer. Enhet, valg, drift, tilkobling av varmeelementer

Tabell 1. Tabell over strømbelastninger

Eksempel 1. Beregn den elektriske varmeren i form av en trådspiral i henhold til den tillatte spesifikke overflateeffekten PF.

Betingelse.Varmereffekt P = 3,5 kW; forsyningsspenning U = 220 V; trådmateriale — nikrom Х20Н80 (en legering av 20 % krom og 80 % nikkel), derfor den spesifikke elektriske motstanden til ledningen ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; temperaturkoeffisient for motstand αр = 16 ∙ 10 ^ (- 6) 1 /ОС; spiralen er åpen, i metallisk form, arbeidstemperaturen til spiralen er Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Bestem d, lp, D, h, n, lp.

Svar. Spolemotstand: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohm.

Spesifikk elektrisk motstand ved Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Finn diameteren på ledningen:

Fra uttrykket R = (ρ ∙ l) ⁄S får vi l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), hvorav lengden på ledningen

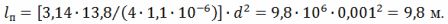
Gjennomsnittlig diameter på spiralvendingen er D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Spiralstigning h = 3 ∙ d = 3 ∙ 1 = 3 mm.

Antall omdreininger i spiralen

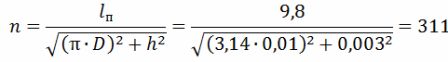
Lengden på helixen er lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Eksempel 2. Beregn strukturelt ledningsmotstandsvarmeren når du bestemmer ledningsdiameteren d ved å bruke tabellen over strømbelastninger (se tabell 1).

Betingelse. Trådvarmereffekt P = 3146 W; forsyningsspenning U = 220 V; trådmateriale — nikrom Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; åpen helix plassert i luftstrømmen (Km = 0,85, Kc = 2,0); tillatt driftstemperatur for lederen Td = 470 ОС.

Bestem diameteren d og lengden på ledningen lp.

Svar.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

Designvarmerstrømmen I = P⁄U = 3146⁄220 = 14,3 A.

I henhold til tabellen over strømbelastninger (se tabell 1) ved Tр = 800 ОС og I = 14,3 A, finner vi diameteren og tverrsnittet til ledningen d = 1,0 mm og S = 0,785 mm2.

Ledningslengde lp = (R ∙ S) ⁄ρ800,

hvor R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ∙11 ] = 1. 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Også, om nødvendig, i likhet med det første eksemplet, kan D, h, n, lsp defineres.

Eksempel 3. Bestem den tillatte spenningen til den rørformede elektriske varmeovnen (TEN).

Tilstand... Batteriet til varmeelementet er laget av nikromtråd med diameter d = 0,28 mm og lengde l = 4,7 m. Varmeelementet er i stilleluft med en temperatur på 20 °C. Kjennetegn på nikrom: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. Lengden på den aktive delen av huset til varmeelementet er La = 40 cm.

Varmeelementet er glatt, ytre diameter dob = 16 mm. Varmeoverføringskoeffisient α = 40 W / (m ^ 2 ∙ ° C). Termiske motstander: fyllstoff RT3 = 0,3 ОС / W, husvegger Rт2 = 0,002 ОС / W.

Bestem hvilken maksimal spenning som kan påføres varmeelementet slik at spoletemperaturen Tsp ikke overstiger 1000 ℃.

Svar. Varmeelementets temperatur på varmeelementet

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

hvor det er omgivelseslufttemperaturen; P er kraften til varmeelementet, W; RT1 — termisk kontaktmotstand for rør-medium-grensesnittet.

Kraften til varmeelementet P = U ^ 2⁄R,

hvor R er motstanden til varmebatteriet.Derfor kan vi skrive Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), hvorfra spenningen på varmeelementet

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Finn R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

hvor ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = (1,12 ) — 6) Ohm • m.

Da er R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Termisk kontaktmotstand RT1 = 1⁄ (α ∙ F),

hvor F er området til den aktive delen av skallet til varmeelementet; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Finn Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Bestem spenningen til varmeelementet U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Hvis den nominelle spenningen som er angitt på varmeelementet er 220 V, vil overspenningen ved Tsp = 1000 OS være 5,6 % ∙ Un.