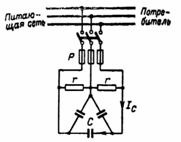
Beregninger for å forbedre effektfaktoren i et trefasenett

Når vi beregner kapasitansen til en kondensator for å forbedre effektfaktoren i et trefasenettverk, vil vi følge samme sekvens som i artikkelen med eksempler på beregninger i et enfaset nett… Verdien av effektfaktoren bestemmes av effektformelen for trefasestrøm:

P1 = √3 ∙ U ∙ I ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ I).

Eksempler av

1. En trefase induksjonsmotor har følgende paneldata: P = 40 kW, U = 380 V, I = 105 A, η = 0,85, f = 50 Hz. Stjernekobling av statoren. Anta at det er vanskelig å bestemme cosφ-verdien til brettet, og derfor er det nødvendig å bestemme den. Til hvilken verdi vil strømmen avta etter å forbedre effektfaktoren til cosφ = 1 ved bruk av kondensatorer? Hvilken kapasitet skal kondensatorene ha? Hvilken reaktiv effekt vil kondensatorene (fig. 1) kompensere for?

Klemmene til statorviklingen er merket: start - henholdsvis C1, C2, C3, slutter - C4, C5, C6.I det følgende, men for å lette kommunikasjonen med diagrammene, vil opprinnelsen merkes A, B, C og endene X, Y, Z.

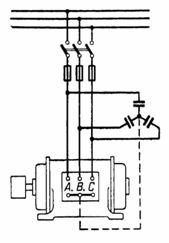
Ris. 1.

Motoreffekt P1 = P2 / η = 40000 / 0,85 ≈47000 W,

hvor P2 er nettoeffekten som er oppført på motorens merkeskilt.

cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0,69.

Etter å ha forbedret effektfaktoren til cosφ = 1, vil inngangseffekten være:

P1 = √3 ∙ U ∙ I ∙ 1

og strømmen vil falle til

I1 = P1 / (√3 ∙ U) = 47000 / (1,73 ∙ 380) = 71,5 A.

Dette er den aktive strømmen ved cosφ = 0,69 siden

Ia = I ∙ cosφ = 105 ∙ 0,69 = 71,5 A.

I fig. 1 viser inkludering av kondensatorer for å forbedre cosφ.

Kondensatorspenning Uph = U / √3 = 380 / √3 = 220 V.

Fasemagnetiseringsstrømmen er lik den lineære magnetiseringsstrømmen: IL = I ∙ sinφ = 105 ∙ 0,75 = 79,8 A.

Den kapasitive motstanden til kondensatoren, som skal gi magnetiseringsstrømmen, vil være: xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).

Derfor er kapasitansen til kondensatoren C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79,8 / (220 ∙ 3,14 ∙ 100) = 79,800 / (22 ∙ 3,14) = ∙ 16,0 = ∙ 16.

En blokk med kondensatorer med en total kapasitet på C = 3 ∙ 1156,4≈3469 μF må kobles til en trefasemotor for å forbedre effektfaktoren til cosφ = 1 og samtidig redusere strømmen fra 105 til 71,5 A.

Den totale reaktive effekten kompensert av kondensatorer, som i fravær av kondensatorer tas fra nettverket, Q = 3 ∙ Uph ∙ IL = 3 ∙ 220 ∙ 79,8≈52668 = 52,66 kvar.

I dette tilfellet bruker motoren aktiv effekt P1 = 47 kW bare fra nettverket.

I fig.2 viser en blokk med kondensatorer koblet i et delta og koblet til terminalene til en trefasemotor hvis vikling også er koblet i et delta. Denne tilkoblingen av kondensatorer er mer fordelaktig enn tilkoblingen vist i fig. 1 (se konklusjonen av beregning 2).

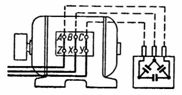
Ris. 2.

2. Et lite kraftverk mater et trefasenett med en strøm I = 250 A ved en nettspenning U = 380 V og en netteffektfaktor cosφ = 0,8. Forbedringen av effektfaktoren oppnås av kondensatorer som er koblet i delta i henhold til diagrammet i fig. 3. Det er nødvendig å bestemme verdien av kapasitansen til kondensatorene og den kompenserte reaktive effekten.

Ris. 3.

Tilsynelatende effekt S = √3 ∙ U ∙ I = 1,73 ∙ 380 ∙ 250 = 164,3 kVA.

Bestem den aktive effekten ved cosφ = 0,8:

P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164,3 ∙ 0,8 = 131,5 W.

Reaktiv effekt som skal kompenseres ved cosφ = 0,8

Q = S ∙ sinφ≈164,3 ∙ 0,6 = 98,6 kvar.

Derfor er den lineære magnetiseringsstrømmen (fig. 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.

Magnetiserende (kapasitiv) fasestrøm ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86,5 A.

Kondensatorstrømmen kan bestemmes på en annen måte av den magnetiserende (reaktive) strømmen i kretsen:

IL = I ∙ sinφ = 250 ∙ 0,6 = 150 A,

ICph = ILph = IL / √3 = 150 / 1,73 = 86,7 A.

Når koblet i et delta, har hver gruppe kondensatorer en spenning på 380 V og en fasestrøm ICph = 86,7 A.

I = ICf = U / xC = U / (1⁄ (ω ∙ C)) = U ∙ ω ∙ C.

Derfor er C = IC / (U ∙ 2 ∙ π ∙ f) = 86,7 / (300 ∙ π ∙ 100) = 726 μF.

Den totale kapasitansen til kondensatorbanken er C3 = 3 ∙ 726 = 2178 μF.

De tilkoblede kondensatorene gjør det mulig å bruke hele kraften til kraftverket S = 164,3 kVA i form av nettoeffekt.Uten driftskondensatorer brukes kun aktiv effekt på 131,5 kW ved cosφ = 0,8.

Den kompenserte reaktive effekten Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 øker proporsjonalt med kvadratet av spenningen. Derfor er den nødvendige kapasiteten til kondensatorene, og dermed kostnadene for kondensatorene, lavere fordi spenningen er høyere.

Motstander r i fig. 3 brukes til å gradvis utlade kondensatorer når de kobles fra nettverket.