Trekkkraften til elektromagneter

Kraften som en elektromagnet tiltrekker seg ferromagnetiske materialer med avhenger av den magnetiske fluksen F eller, tilsvarende, av induksjonen B og tverrsnittsarealet til elektromagneten S.

Trykkkraften til elektromagneten bestemmes av formelen

F = 40550 ∙ B ^ 2 ∙ S,

hvor F er trykkkraften til elektromagneten, kg (kraften måles også i newton, 1 kg = 9,81 N eller 1 N = 0,102 kg); B - induksjon, T; S er tverrsnittsarealet til elektromagneten, m2.

Eksempler av

1. Kranen elektromagnet er en magnetisk krets (fig. 1). Hva er løftekraften til en hesteskokranelektromagnet, hvis den magnetiske induksjonen er B = 1 T, og tverrsnittsarealet til hver pol av elektromagneten er S = 0,02 m2 (fig. 1, b)? Overse effekten av gapet mellom elektromagneten og ankeret.

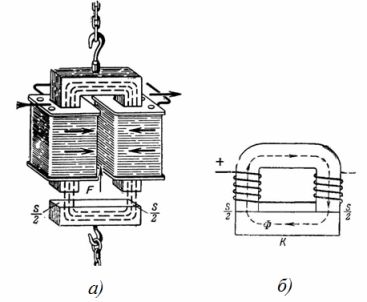
Ris. 1. Løfte elektromagnet

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

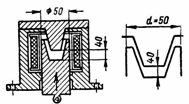
2. En sirkulær stålelektromagnet har dimensjonene vist i fig. 2, a og b. Løftekraften til elektromagneten er 3 T. Bestem tverrsnittsarealet til elektromagnetkjernen, n. p. og antall omdreininger av spolen ved en magnetiseringsstrøm I = 0,5 A.

Ris. 2. Rund elektromagnet

Den magnetiske fluksen passerer gjennom den sirkulære indre kjernen og går tilbake gjennom den sylindriske kroppen. Tverrsnittsarealene til kjernen Sc og foringsrøret Sk er omtrent det samme, derfor er induksjonsverdiene i kjernen og foringsrøret praktisk talt de samme:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

Den nødvendige induksjonen i elektromagneten bestemmes av formelen F = 40550 ∙ B ^ 2 ∙ S,

hvor B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

Spenningen ved denne induksjonen finnes på magnetiseringskurven til støpestålet:

H = 180 A/m.

Gjennomsnittlig lengde på feltlinjen (fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Magnetiseringskraft I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.

Egentlig n. s, det vil si strømmen og antall omdreininger, må være mange ganger større, siden det er et uunngåelig luftgap mellom elektromagneten og ankeret, noe som betydelig øker den magnetiske motstanden til den magnetiske kretsen. Derfor må luftgapet tas i betraktning ved beregning av elektromagnetene.

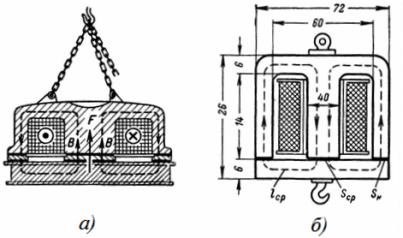
3. Spolen til elektromagneten for kranen har 1350 omdreininger, gjennom den strømmer en strøm I = 12 A. Dimensjonene til elektromagneten er vist i fig. 3. Hvilken vekt løfter elektromagneten i en avstand på 1 cm fra ankeret og hvilken vekt kan den holde etter tyngdekraften?

Ris. 3. Elektromagnetisk spole

Mesteparten av N. med I ∙ ω brukes på å lede magnetisk fluks gjennom luftgapet: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Magnetiseringskraft I ∙ ω = 12 ∙ 1350 = 16200 A.

Siden H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, så Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Derfor er 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, dvs. B = 1,012T.

Vi antar at induksjonen er B = 1 T, siden en del av n. c. I ∙ ω brukes på å lede magnetisk fluks i stål.

La oss sjekke denne beregningen med formelen I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

Den gjennomsnittlige lengden på magnetlinjen er: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

Intensiteten Hc ved B = 1 T (10000 Gs) bestemmes fra magnetiseringskurven:

Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

Magnetiseringskraften I ∙ ω = 16114 Av som skaper en induksjon B = 1 T er praktisk talt lik den gitte n. v. I ∙ ω = 16200 Av.

Det totale tverrsnittsarealet til kjernen og kjeglen er: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

Elektromagneten vil tiltrekke seg en ladning med vekt F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg fra en avstand på 1 cm.

Siden luftgapet praktisk talt forsvinner etter at ankeret er tiltrukket, tåler elektromagneten en mye større belastning. I dette tilfellet vil hele n. c. I ∙ ω brukes på å lede magnetisk fluks kun i stål, derfor I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

Ved en slik spenning er stålet praktisk talt mettet og induksjonen i det er omtrent 2 T. Elektromagneten tiltrekker ankeret med en kraft F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. Signalreléet (blinker) består av en pansret elektromagnet 1 med en rund kjerne og et anker 2 av ventiltypen, som etter å ha tilført strøm til elektromagneten tiltrekker og frigjør blinklyset 3, som åpner signalsifferet (fig. 4).

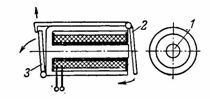
Ris. 4. Panserelektromagnet

Magnetiseringsstyrken er I ∙ ω = 120 Av, luftgapet er δ = 0,1 cm, og det totale tverrsnittsarealet til elektromagneten er S = 2 cm2. Beregn trekkkraften til reléet.

Induktans B bestemmes ved suksessive tilnærminger ved å bruke ligningen I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

La n. c. Hc ∙ lc er 15 % I ∙ ω, dvs. 18 Av.

Da I ​​∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = H6 ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Derfor finner vi induksjon B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Etter å ha erstattet verdien B i formelen F = 40550 ∙ B ^ 2 ∙ S, får vi:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

5. DC-bremsesolenoiden (fig. 5) har et stempelanker med en konisk stopp. Avstanden mellom armatur og kjerne er 4 cm Arbeidsdiameter (kjerner med sirkulær kontaktflate) d = 50 mm. Armaturet trekkes inn i spolen med en kraft på 50 kg. Lengden på midtkraftlinjen lav = 40 cm Bestem n. s. og spolestrømmen hvis det er 3000 omdreininger.

Ris. 5. DC-bremsesolenoid

Arealet av elektromagnetens arbeidsseksjon er lik arealet av en sirkel med diameter d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

Induksjonen B som kreves for å skape en kraft F = 50 kg er funnet fra ligningen F = 40550 ∙ B ^ 2 ∙ S,

hvor B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Magnetiseringskraft I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Vi bestemmer magnetiseringsstyrken for stål Hc ∙ lc på en forenklet måte, basert på at den er 15 % I ∙ ω:

I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30 000 Av.

Magnetiseringsstrøm I = (I ∙ ω) / ω = 30000/3000 = 10 A.