Batterier. Regneeksempler

Batterier er elektrokjemiske strømkilder som etter utlading kan lades ved hjelp av elektrisk strøm hentet fra en lader. Når ladestrømmen flyter i batteriet, oppstår elektrolyse, som et resultat av at det dannes kjemiske forbindelser på anoden og katoden som var på elektrodene i den opprinnelige driftstilstanden til batteriet.

Elektrisk energi, når den lades i et batteri, omdannes til en kjemisk form for energi. Når den utlades, blir den kjemiske formen for energi elektrisk. Det tar mer energi å lade et batteri enn det man kan få ved å lade det ut.

Spenningen til hver celle i et blybatteri etter lading av 2,7 V bør ikke synke under 1,83 V ved utlading.

Den gjennomsnittlige spenningen til et nikkel-jernbatteri er 1,1 V.

Lade- og utladingsstrømmene til batteriet er begrenset og innstilt av produsenten (ca. 1 A per 1 dm2 av platen).

Mengden elektrisitet som kan trekkes fra et ladet batteri kalles batteriets ampere-timekapasitet.

Batterier er også preget av energi- og strømeffektivitet.Energiavkastningen er lik forholdet mellom energien mottatt under utlading og energien som brukes på å lade batteriet: ηen = Araz / Azar.

For et blybatteri ηen = 70 % og for et jern-nikkelbatteri ηen = 50 %.

Strømutgangen er lik forholdet mellom mengden elektrisitet mottatt under utlading og mengden elektrisitet som forbrukes under lading: ηt = Q ganger / Qchar.

Blybatterier har ηt = 90 % og jern-nikkelbatterier ηt = 70 %.

Batteriberegning

1. Hvorfor er strømavkastningen til batteriet større enn energiavkastningen?

ηen = Araz / Azar = (Opp ∙ Ip ∙ tp) / (Uz ∙ Iz ∙ tz) = Opp / Uz ∙ ηt.

Energiavkastningen er lik strømavkastningen ηt multiplisert med forholdet mellom utladningsspenningen og ladespenningen. Siden forholdet Uр / U3 <1, så ηen <ηt.

2. Et blybatteri med en spenning på 4 V og en kapasitet på 14 Ah er vist i fig. 1. Tilkoblingen av platene er vist i fig. 2. Parallellkobling av platene øker batterikapasiteten. To sett med plater er koblet i serie for å øke spenningen.

Ris. 1. Bly-syre batteri

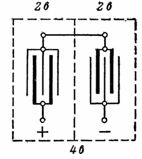
Ris. 2. Koble til platene til et bly-syrebatteri for en spenning på 4 V

Batteriet lades på 10 timer med en strøm på Ic = 1,5 A og utlades på 20 timer med en strøm på Ip = 0,7 A. Hva er strømeffektiviteten?

Qp = Ip ∙ tp = 0,7 ∙ 20 = 14 A • h; Qz = Iz ∙ tz = 1,5 ∙ 10 = 15 A • h; ηt = Qp / Qz = 14/15 = 0,933 = 93%.

3. Batteriet lades med en strøm på 0,7 A i 5 timer. Hvor lenge vil den utlades med en strøm på 0,3 A med en strømutgang ηt = 0,9 (fig. 3)?

Ris. 3. Figur og diagram for eksempel 3

Mengden elektrisitet som brukes til å lade batteriet er: Qz = Iz ∙ tz = 0,7 ∙ 5 = 3,5 A • h.

Mengden elektrisitet Qp som frigjøres under utlading, beregnes med formelen ηt = Qp / Qz, hvorfra Qp = ηt ∙ Qz = 0,9 ∙ 3,5 = 3,15 A • h.

Utladningstid tp = Qp / Ip = 3,15 / 0,3 = 10,5 timer.

4. 20 Ah-batteriet ble fulladet innen 10 timer fra strømnettet via en selenlikeretter (fig. 4). Den positive polen på likeretteren er koblet til den positive polen på batteriet under lading. Med hvilken strøm lades batteriet hvis strømeffektiviteten ηt = 90 %? Med hvilken strøm kan batteriet lades ut innen 20 timer?

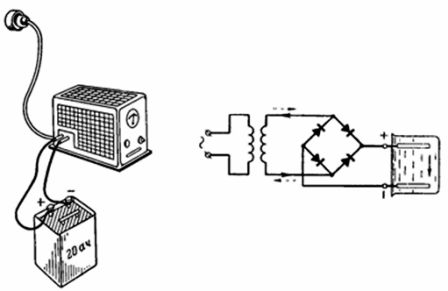
Ris. 4. Figur og diagram for eksempel 4

Batteriladestrømmen er: Ic = Q / (ηt ∙ tc) = 20 / (10 ∙ 0,9) = 2,22 A. Tillatt utladningsstrøm Iр = Q / tr = 20/20 = 1 A.

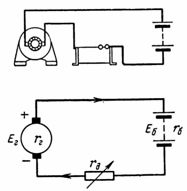
5. Et akkumulatorbatteri bestående av 50 celler lades med en strøm på 5 A. en battericelle 2,1 V, og dens indre motstand rvn = 0,005 Ohm. Hva er batterispenningen? Hva er etc. c. må ha en ladegenerator med intern motstand rg = 0,1 Ohm (fig. 5)?

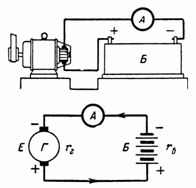
Ris. 5. Figur og diagram for eksempel 5

D. d. C. batteri er lik: Eb = 50 ∙ 2,1 = 105 V.

Intern motstand til batteriet rb = 50 ∙ 0,005 = 0,25 Ohm. D. d. S. generator er lik summen av e. etc. med batterier og spenningsfall i batteri og generator: E = U + I ∙ rb + I ∙ rg = 105 + 5 ∙ 0,25 + 5 ∙ 0,1 = 106,65 V.

6. Lagringsbatteriet består av 40 celler med intern motstand rvn = 0,005 Ohm og e. etc. s. 2,1 V. Batteriet lades med strøm I = 5 A fra generatoren, f.eks. etc. medsom er 120 V og den indre motstanden rg = 0,12 Ohm. Bestem den ekstra motstanden rd, kraften til generatoren, den nyttige kraften til ladningen, effekttapet i den ekstra motstanden rd og krafttapet i batteriet (fig. 6).

Ris. 6. Beregning av akkumulatoren

Finn ytterligere motstand ved å bruke Kirchhoffs andre lov:

F.eks = Eb + rd ∙ I + rg ∙ I + 40 ∙ rv ∙ I; rd = (Eg-Eb-I ∙ (rg + 40 ∙ rv)) / I = (120-84-5 ∙ (0,12 + 0,2)) / 5 = 34,4 / 5 = 6,88 Ohm …

Siden e. etc. c. Når batteriet er ladet, er EMF til cellen ved begynnelsen av ladingen 1,83V, deretter ved begynnelsen av ladingen, med en konstant tilleggsmotstand, vil strømmen være mer enn 5 A. For å opprettholde en konstant lading strøm, er det nødvendig å endre den ekstra motstanden.

Effekttap i tilleggsmotstanden ∆Pd = rd ∙ I ^ 2 = 6,88 ∙ 5 ^ 2 = 6,88 ∙ 25 = 172 W.

Effekttap i generatoren ∆Pg = rg ∙ I ^ 2 = 0,12 ∙ 25 = 3 W.

Strømtap i batteriets indre motstand ∆Pb = 40 ∙ rvn ∙ I ^ 2 = 40 ∙ 0,005 ∙ 25 = 5 W.

Den tilførte effekten fra generatoren til den eksterne kretsen er Pg = Eb ∙ I + Pd + Pb = 84 ∙ 5 + 172 + 5 = 579 W.

Nyttig ladeeffekt Ps = Eb ∙ I = 420 W.