Enfaset vekselstrøm

Får vekselstrøm

Hvis ledningen A roteres i den magnetiske fluksen som dannes av magnetens to poler i retning med klokken (fig. 1), så når ledningen krysser magnetfeltlinjene, vil den indusere e. d. s hvis verdi bestemmes av uttrykket

E = Blvsinα,

hvor B er den magnetiske induksjonen i T, l er lengden på ledningen i m, v er ledningens hastighet i m/s, α — vinkelen som ledningen krysser de magnetiske feltlinjene med.

La B, I og v for dette tilfellet forbli konstant, så den induserte e. etc. c. vil kun avhenge av vinkelen α hvor ledningen krysser magnetfeltet. Så, ved punkt 1, når ledningen beveger seg langs magnetfeltlinjene, vil verdien av den induserte emf. etc. p vil være null når ledningen beveger seg til punkt 3 oe. etc. v. vil være av størst betydning, siden kraftlinjene vil krysses av lederen i retningen vinkelrett på dem, og til slutt, f.eks. etc. v. vil igjen nå null hvis ledningen flyttes til punkt 5.

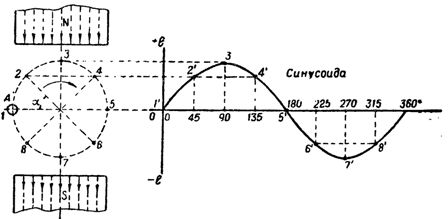
Ris. 1. Endre den induserte e. etc. s. i en ledning som roterer i et magnetfelt

Ved mellompunktene 2 og 4, der ledningen krysser kraftlinjene i en vinkel α = 45 °, er verdien av den induserte emf. etc. c. vil være tilsvarende mindre enn ved punkt 3. Således, når ledningen dreies fra punkt 1 til punkt 5, dvs. med 180°, vil den induserte e. etc. v. endres fra null til maksimum og tilbake til null.

Det er ganske åpenbart at ved en ytterligere rotasjon av ledningen A gjennom en vinkel på 180 ° (gjennom punktene 6, 7, 8 og 1), vil arten av endringen i den induserte e. etc. p. vil være den samme, men dens retning vil endres til motsatt, siden ledningen vil krysse magnetfeltlinjene allerede under den andre polen, noe som tilsvarer å krysse dem i motsatt første retning.

Derfor, når ledningen roteres 360 °, vil den induserte e. etc. v. endres ikke bare i størrelse hele tiden, men endrer også retning to ganger.

Hvis ledningen er lukket for en viss motstand, vil ledningen vises elektrisitet, også varierende i størrelse og retning.

Elektrisk strøm, som kontinuerlig endrer seg i størrelse og retning, kalles vekselstrøm.

Hva er en sinusbølge?

Arten av endringen e. etc. (strøm) for en omdreining av ledningen for større klarhet, er de grafisk representert ved hjelp av en kurve. Siden verdien av e. etc. c. proporsjonal med sinα, da, etter å ha satt visse vinkler, er det mulig, ved hjelp av tabeller, å bestemme verdien av sinusen til hver vinkel, og på passende skala å konstruere en kurve for endringen av e. etc. c. For å gjøre dette vil vi på den horisontale aksen sette til side rotasjonsvinklene til ledningen, og på den vertikale aksen, i passende skala, den induserte e. etc. med

Hvis tidligere angitt i fig.1 koble punktene med en jevn buet linje, så vil det gi en ide om størrelsen og arten av endringen i den induserte e. etc. (strøm) ved enhver posisjon av lederen i et magnetfelt. På grunn av det faktum at verdien av den induserte e. etc. p. til enhver tid bestemmes av sinusen til vinkelen som ledningen krysser magnetfeltet vist i fig. 1 kurve kalles en sinusformet, og f.eks. etc. s. — sinusformet.

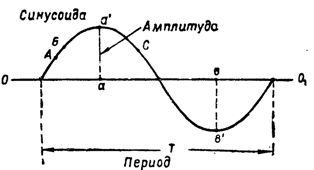
Ris. 2. Sinusoiden og dens karakteristiske verdier

Endringene vi så på f.eks. etc. c. sinusformet tilsvarer ledningens rotasjon i et magnetfelt i en vinkel på 360 °. Når ledningen roteres de neste 360 ​​°, vil endringene i indusert e. etc. s.(og strøm) vil vises igjen i en sinusbølge, det vil si at de vil gjentas med jevne mellomrom.

Følgelig, forårsaket av denne e. etc. c. kalles elektrisk strøm sinusformet vekselstrøm... Det er ganske åpenbart at spenningen som kan måles av oss i endene av ledning A, i nærvær av en lukket ekstern krets, også vil endre seg på en sinusformet måte.

Vekselstrøm oppnådd ved å rotere en ledning i en magnetisk fluks eller et system av ledninger koblet i en spole kalles enfaset vekselstrøm.

Sinusformede vekselstrømmer er de mest brukte innen teknologi. Du kan imidlertid finne vekselstrømmer som ikke endres i henhold til sinusloven. Slike vekselstrømmer kalles ikke-sinusformet.

Se også: Hva er vekselstrøm og hvordan skiller den seg fra likestrøm

Amplitude, periode, frekvens for enfaset vekselstrøm

Nåværende styrke, endres langs en sinusoid, endres kontinuerlig. Så hvis ved punkt A (fig. 2) strømmen er lik 3a, vil den allerede i punkt B være større.På et annet punkt på sinusoiden, for eksempel ved punkt C, vil strømmen nå ha en ny verdi, og så videre.

Styrken til strømmen på bestemte tidspunkter når den endres langs en sinusformet kalles øyeblikkelige strømverdier.

Den største øyeblikkelige verdien av en enfaset vekselstrøm kalles når den endrer seg langs en sinusformet amplitude... Det er lett å se at for en omdreining av ledningen når strømmen sin amplitudeverdi to ganger. En av verdiene til aa 'er positiv og er trukket opp fra 001-aksen og den andre bv' er negativ og trekkes ned fra aksen.

Tiden da den induserte e. etc. (eller strømkraften) går gjennom hele endringssyklusen, den såkalte månedlige syklusen T (fig. 2). Perioden måles vanligvis i sekunder.

Periodens gjensidige kalles frekvensen (f). Med andre ord, vekselstrømsfrekvens er antall perioder per tidsenhet, dvs. på sekunder. Så, for eksempel, hvis en vekselstrøm innen 1 sekund antar samme verdier og retning ti ganger, vil frekvensen til en slik vekselstrøm være 10 perioder per sekund.

For å måle frekvens, i stedet for antall perioder per sekund, brukes en enhet kalt hertz (hertz). En frekvens på 1 hertz er lik en frekvens på 1 lps/sek. Ved måling av høye frekvenser er det mer praktisk å bruke en enhet 1000 ganger større enn hertz, dvs. kilohertz (kHz), eller 1 000 000 ganger større enn hertz - megahertz (mhz).

Vekselstrømmer brukt i teknologi, avhengig av frekvens, kan deles inn i lavfrekvente strømmer og høyfrekvente strømmer.

AC rms verdi

Likestrøm som går gjennom ledningen varmer den opp. Hvis du kjører vekselstrøm gjennom ledningen, vil ledningen også varmes opp.Dette er forståelig, for selv om vekselstrømmen endrer retning hele tiden, avhenger ikke varmeavgivelsen i det hele tatt av strømmens retning i ledningen.

Når vekselstrøm føres gjennom en lyspære, vil glødetråden lyse. Ved en standard vekselstrømfrekvens på 50 Hz vil det ikke være flimring av lyset, fordi glødepærens glødetråd, som har termisk treghet, ikke har tid til å kjøle seg ned på de tidspunktene når strømmen i kretsen er null. Bruk av vekselstrøm med en frekvens på mindre enn 50 Hz for belysning er nå uønsket på grunn av det faktum at det oppstår ubehagelige, øyetrettende svingninger i pærens intensitet.

Hvis vi fortsetter likestrømsanalogien, kan vi forvente at en vekselstrøm som flyter gjennom en ledning skaper rundt den magnetfelt. Egentlig nVekselstrøm skaper ikke et magnetfelt, men fordi magnetfeltet den skaper vil også være variabel i retning og størrelse.

En vekselstrøm endres hele tiden i både størrelse og retningNS. Naturligvis oppstår spørsmålet om hvordan man måler variabelen T-brønn, og hvilken verdi dens når man skifter langs en sinusoide bør tas som årsak til denne eller den handlingen.

C Til dette formål sammenlignes vekselstrøm med hensyn til virkningen den produserer med likestrøm, hvis verdi forblir uendret under eksperimentet.

Anta at en likestrøm flyter gjennom en ledning med konstant motstand 10 A og det er funnet at ledningen varmes opp til en temperatur på 50 °.Hvis vi nå passerer gjennom den samme ledningen ikke en likestrøm, men en vekselstrøm, og så velger vi verdien (virker for eksempel med en reostat) slik at ledningen også varmes opp til en temperatur på 50 °, så i i dette tilfellet kan vi si at virkningen av vekselstrøm er lik virkningen av likestrøm.

Oppvarming av ledningen i begge tilfeller til samme temperatur viser at i en tidsenhet avgir vekselstrømmen i ledningen like mye varme som likestrømmen.

En sinusformet vekselstrøm som avgir for en gitt motstand per tidsenhet samme mengde varme som en likestrøm som i størrelsesorden tilsvarer en likestrøm... Denne strømverdien kalles den effektive (Id) eller effektive verdien av vekselstrøm .. Derfor, for vårt eksempel, vil den effektive verdien av vekselstrøm være 10 A... I dette tilfellet vil de maksimale (topp) strømverdiene overstige gjennomsnittsverdiene i størrelsesorden.

Erfaring og beregninger viser at de effektive verdiene for vekselstrøm er mindre enn dens amplitudeverdier i √2 (1,41) ganger. Derfor, hvis toppverdien til strømmen er kjent, kan den effektive verdien av strømmen Id bestemmes ved å dele amplituden til strømmen Ia med √2, dvs. Id = Aza/√2

Omvendt, hvis rms-verdien til strømmen er kjent, kan toppverdien til strømmen beregnes, dvs. Ia = Azd√2

De samme relasjonene vil gjelde for amplituden og rms-verdiene til e. etc. v. og spenninger: Enhet = Ea /√2, Ud = Uа/√2

Måleenheter viser oftest de faktiske verdiene, derfor, når notasjon, er indeksen «d» vanligvis utelatt, men du bør ikke glemme det.

Impedans i AC-kretser

Når induktans- og kapasitansforbrukere er koblet til AC-kretsen, må både aktiv og reaktans vurderes (reaktans oppstår når en kondensator er på eller struper i en AC-krets). Derfor, når du bestemmer strømmen som går gjennom en slik forbruker, er det nødvendig å dele forsyningsspenningen med impedansen til kretsen (forbrukeren).

Impedansen (Z) til en enfaset AC-krets bestemmes av følgende formel:

Z = √(R2 + (ωL — 1 / ωC)2

der R er den aktive motstanden til kretsen i ohm, L er induktansen til kretsen i henries, C er kapasitansen til kretsen (kondensatoren) i farad, ω — vinkelfrekvensen til vekselstrøm.

Ulike forbrukere brukes i vekselstrømkretser der det er nødvendig å vurdere enten de tre verdiene til R, L, C eller bare noen av dem. Samtidig må det tas hensyn til vinkelfrekvensen til vekselstrømmen.

For noen brukere kan bare verdiene til R og L tas i betraktning ved de tilsvarende hjørnefrekvensverdiene. For eksempel ved en AC-frekvens på 50 Hz magnetspole eller generatorviklingen kan bare anses å inneholde aktiv og induktiv motstand. Med andre ord kan kapasitansen i dette tilfellet neglisjeres. Deretter kan AC-impedansen til en slik bruker beregnes med formelen:

Z = √(R2 + ω2L2)

Hvis en slik spole eller en spole konstruert for vekselstrømsdrift kobles til en likestrøm med samme spenning, vil det flyte en veldig stor strøm gjennom spolen, noe som kan føre til betydelig varmeutvikling, og spolens isolasjon kan bli skadet Tvert imot vil en liten strøm flyte gjennom en spole designet for å fungere i en likestrømskrets og koblet til en vekselstrømkrets med samme spenning, og enheten som denne spolen brukes i vil ikke utføre den nødvendige handlingen.

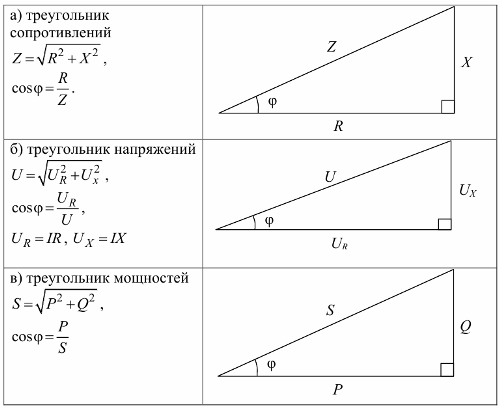
Motstandstrekant, spenningstrekant og krafttrekant: