Aktiv motstand og induktor i AC-krets

Vurderer en AC-krets som bare inneholder induktiv motstand (se artikkelen «Induktor i en vekselstrømkrets»), antok vi at den aktive motstanden til denne kretsen er null.

Faktisk har både ledningen til selve spolen og tilkoblingsledningene en liten, men aktiv motstand, så kretsen bruker uunngåelig energien til strømkilden.

Derfor, når du bestemmer den totale motstanden til en ekstern krets, er det nødvendig å legge til dens reaktive og aktive motstander. Men det er umulig å legge til disse to motstandene som er forskjellige i naturen.

I dette tilfellet blir impedansen til kretsen til vekselstrømmen funnet ved geometrisk addisjon.

En rettvinklet trekant (se figur 1) er konstruert, hvor den ene siden er verdien av den induktive motstanden, og den andre siden er verdien av den aktive motstanden. Den ønskede kretsimpedansen bestemmes av den tredje siden av trekanten.

Figur 1. Bestemmelse av impedansen til en krets som inneholder induktiv og aktiv motstand

Kretsimpedansen er angitt med den latinske bokstaven Z og måles i ohm. Det kan ses av konstruksjonen at den totale motstanden alltid er større enn den induktive og aktive motstanden tatt hver for seg.

Det algebraiske uttrykket for den totale kretsmotstanden er:

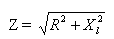
hvor Z - total motstand, R - aktiv motstand, XL - induktiv motstand til kretsen.

Derfor er den totale motstanden til en krets mot vekselstrøm, bestående av aktiv og induktiv motstand, lik kvadratroten av summen av kvadratene av den aktive og induktive motstanden til denne kretsen.

Ohms lov siden en slik krets er uttrykt med formelen I = U / Z, hvor Z er den totale motstanden til kretsen.

La oss nå analysere hva spenningen blir dersom kretsen i tillegg til og og faseforskyvningen mellom strømmen og induktansen også har en relativt stor aktiv motstand. I praksis kan en slik krets for eksempel være en krets som inneholder en jernkjerne-induktor viklet av en tynn ledning (høyfrekvent choke).

I dette tilfellet vil faseforskyvningen mellom strøm og spenning ikke lenger være en kvart periode (som det var i en krets med kun induktiv motstand), men mye mindre; og jo større motstand, jo mindre faseforskyvning vil resultere.

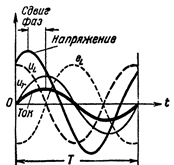
Figur 2. Strøm og spenning i en krets som inneholder R og L.

Nå er hun selv EMF av selvinduksjon er ikke i motfase med strømkildespenningen, da den er forskjøvet i forhold til spenningen ikke med en halv periode, men med mindre.I tillegg er spenningen skapt av strømkilden ved spolens terminaler ikke lik emf for selvinduksjon, men er større enn den med mengden av spenningsfallet i den aktive motstanden til spoleledningen. Med andre ord består spenningen i spolen uansett av to komponenter:

• tiL- den reaktive komponenten av spenningen, som balanserer effekten av EMF fra selvinduksjon,

• tiR- den aktive komponenten av spenningen som vil overvinne den aktive motstanden til kretsen.

Kobler vi en stor aktiv motstand i serie med spolen, vil faseforskyvningen avta så mye at den nåværende sinusbølgen nesten vil hamle opp med spenningens sinusbølge og forskjellen i fasene mellom dem vil knapt være merkbar.I dette tilfellet amplituden til begrepet og vil være større enn amplituden til begrepet.

På samme måte kan du redusere faseforskyvningen og til og med redusere den helt til null hvis du reduserer frekvensen til generatoren på en eller annen måte. En reduksjon i frekvens vil resultere i en reduksjon i selvinduksjons-EMK og derfor en reduksjon i faseforskyvningen mellom strømmen og spenningen i kretsen forårsaket av den.

Kraften til en AC-krets som inneholder en induktor

Vekselstrømkretsen som inneholder spolen forbruker ikke energien til strømkilden og at det i kretsen er en energiutvekslingsprosess mellom generatoren og kretsen.

La oss nå analysere hvordan ting vil være med strømmen som forbrukes av en slik ordning.

Strømmen som forbrukes i en AC-krets er lik produktet av strøm og spenning, men siden strøm og spenning er variable størrelser, vil også effekten være variabel.I dette tilfellet kan vi bestemme effektverdien for hvert øyeblikk i tid hvis vi multipliserer strømverdien med spenningsverdien som tilsvarer et gitt tidspunkt.

For å få effektgrafen må vi multiplisere verdiene til de rette linjesegmentene som definerer strømmen og spenningen til forskjellige tider. En slik konstruksjon er vist i fig. 3, a. Den stiplede bølgeformen p viser oss hvordan effekten endres i en AC-krets som kun inneholder induktiv motstand.

Følgende algebraiske multiplikasjonsregel ble brukt til å konstruere denne kurven: Når en positiv verdi multipliseres med en negativ verdi, oppnås en negativ verdi, og når to negative eller to positive verdier multipliseres, oppnås en positiv verdi.

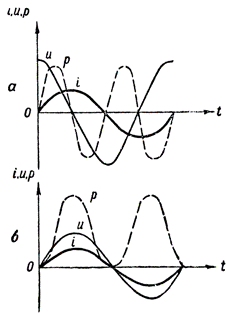
Figur 3. Effektgrafer: a — i en krets som inneholder induktiv motstand, b — også aktiv motstand

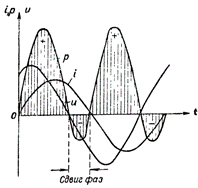
Figur 4. Effektplott for en krets som inneholder R og L.

Effektkurven i dette tilfellet ligger over tidsaksen. Dette betyr at det ikke er noen utveksling av energi mellom generatoren og kretsen, og derfor forbrukes kraften som tilføres av generatoren til kretsen fullstendig av kretsen.

I fig. 4 viser effektdiagrammet for en krets som inneholder både induktiv og aktiv motstand. I dette tilfellet skjer også omvendt overføring av energi fra kretsen til strømkilden, men i mye mindre grad enn i en krets med en enkelt induktiv motstand.

Etter å ha gjennomgått effektgrafene ovenfor, konkluderer vi med at bare faseforskyvningen mellom strøm og spenning i kretsen skaper "negativ" effekt.I dette tilfellet, jo større faseforskyvningen mellom strømmen og spenningen i kretsen er, desto mindre strøm vil kretsen forbruke, og omvendt, jo mindre faseforskyvningen er, desto større kraft forbrukes av kretsen.

Les også: Hva er spenningsresonans