Punktmetode for lysberegning

Punktmetoden gjør det mulig å bestemme belysningsstyrken på ethvert punkt i rommet både i horisontalt og vertikalt eller skråplanet.

Generelt benyttes en punktmetode for beregning av belysning ved beregning av lokalisert og utendørs belysning i tilfeller hvor noen av lysarmaturene er dekket av utstyr plassert i rommet, ved belysning av skrå eller vertikale flater, samt ved beregning av belysning av industrielt lokaler med mørke vegger og tak (støperier, smeder, de fleste butikker av metallurgiske anlegg, etc.).

Punktmetoden er basert på ligningen knyttet til belysningsstyrke og lysintensitet:

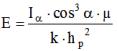
hvor: azα — lysintensitet i retning fra kilden til et gitt punkt på arbeidsflaten (bestemt av lysintensitetskurvene eller tabellene for den valgte typen lysarmaturer), α — vinkelen mellom normalen til arbeidsflaten og retningen av lysintensiteten til det beregnede punktet, er μ en koeffisient som tar hensyn til effekten av lysarmaturer fjernt fra designpunktet og den reflekterte lysstrømmen fra vegger, tak, gulv, utstyr som faller på arbeidsflaten ved designpunkt (tatt innenfor μ = 1,05 ... 1 ,2), k er sikkerhetsfaktoren, hk er høyden på armaturopphenget over arbeidsflaten.

Før du starter punktbelysningsberegningen, er det nødvendig å tegne en skala over plasseringen av belysningsarmaturene for å bestemme de geometriske forholdene og vinklene.

Beregningen ved poengmetoden er mer komplisert enn beregningen av den spesifikke kraften og utnyttelsesgradsmetode... Beregningen utføres etter spesielle formler, nomogrammer, grafer og hjelpetabeller.

Det enkleste er å bestemme belysningsstyrken i horisontalplanet fra lysarmaturer ved hjelp av LN romlige isolux-grafer... Slike grafer er bygget for hver type lysarmaturer og er tilgjengelig i oppslagsverk for elektrisk lysdesign. «Isolux» er en linje som forbinder punkter med samme belysning.

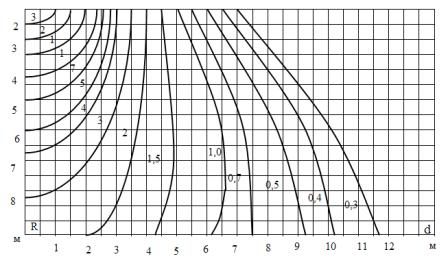
I fig. 1 viser den vertikale aksen armaturens høyde over den beregnede overflaten h i meter og den horisontale aksen viser avstanden d i meter 30, 20, 15, 10, 7 … — hver kurve har belysningen i lux for armaturen som har en lysflukslampe, lik 1000 lm.

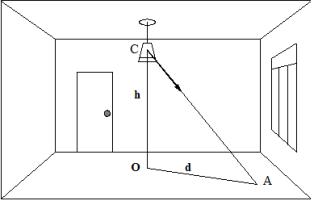
For å forstå formålet med den romlige isoluxen og essensen av beregningen basert på dem, la oss lage en enkel tegning (fig. 2). La lysarmaturen C monteres i rommet i høyde h over beregnet overflate, for eksempel over gulvet. La oss ta punkt A på gulvet, hvor det er nødvendig å bestemme belysningsstyrken. La oss angi avstanden fra projeksjonen av lysarmaturen på det beregnede planet O til punkt A med d.

For å bestemme belysningsstyrken ved punkt A, må du kjenne verdiene til h og d. Anta at h = 4 m, d = 6 m. I fig. 2 tegne en horisontal linje fra tallet 4 på den vertikale aksen og en vertikal linje fra tallet 6 på den horisontale aksen. Linjene skjærer hverandre i punktet som kurven går gjennom, markert med tallet 1. Dette betyr at i punkt A skaper armaturet C en betinget belysning e = 1 lux.

Ris. 1. Romlig isoluks av betinget horisontal belysning fra en lysarmatur med frostet glass.

Ris. 2. Til beregning av belysning ved punktmetoden. C — lysarmatur, O — projeksjon av lysarmaturen på det beregnede planet, A — kontrollpunkt.

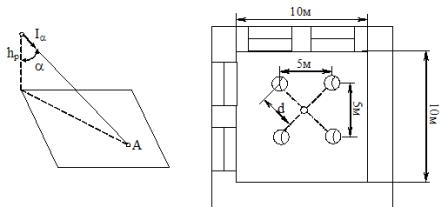
Ris. 3. Til beregning av belysning ved punktmetoden

Beregningen av belysningsstyrken ved punktmetoden fra lysarmaturer med symmetrisk lysfordeling (fig. 3) anbefales utført i følgende rekkefølge:

1. I henhold til forholdet d / hp bestemmes tga og derfor vinkelen α og cos3α, hvor d er avstanden fra designpunktet til projeksjonen av symmetriaksen til lysarmaturen på et plan vinkelrett på den og passerer gjennom designpunktet.

2. Ia velges i henhold til lysintensitetskurven (eller tabelldata) for den valgte typen lysarmaturer og vinkel a.

3.Grunnformelen brukes til å beregne den horisontale belysningen fra hver lysarmatur på det beregnede punktet.

4. Bestem den totale belysningen ved kontrollpunktet skapt av alle armaturene.

5. Beregn den estimerte lysstrømmen (i lumen) som må skapes av hver lampe for å oppnå den nødvendige (normaliserte) belysningsstyrken ved det beregnede punktet.

6. Basert på den beregnede lysfluksen, velg en lampe med nødvendig effekt.

Et eksempel på beregning av belysning ved punktmetoden

Et rom med et areal på 100 m2 og en høyde på 5 m er opplyst av fire lamper av typen RSP113-400 med 400 W DRL-lamper. Lysarmaturene er plassert i hjørnene av en firkant med en side på 5 m (fig. 2). Høyden på opphenget av belysningsenheten over arbeidsflaten er k.s. = 4,5 m. Normalisert belysning ved kontrollpunkt A er 250 lux. Bestem om belysningen ved kontrollpunktet er innenfor den nødvendige normen.

1. Bestem tgα (fig. 3), α og cos3α , α= 37 °, cos3α=0,49.

2. Bestem Ia. I henhold til lysintensitetskurven til RSP13-armaturer (DRL) med en konvensjonell lampe med en lysstrøm ФL = 1000 lm, finner vi lysintensiteten Ia ved α = 37 ° (interpolasjon mellom lysintensitetsverdiene for vinkelen α = 35° og 45°), Ia1000 = 214 cd.

Lysstrømmen til en 400 W DRL-lampe installert i armaturen er 19 000 lm. Derfor Ia = 214 × (19000/1000) = 214 × 19 = 4066 cd.

3. Vi beregner belysningen fra en lysarmatur i horisontalplanet ved kontrollpunkt A. Tar vi sikkerhetsfaktoren k = 1,5 for en lysarmatur og μ = 1,05 får vi

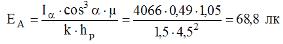
Siden ved designpunktet hver av de fire lampene produserer samme belysning, vil den totale horisontale belysningen ved punkt A være ∑EA = 4 × 68,8 = 275,2 lux

Den faktiske belysningen øker den normaliserte (250 lux) med ca. 10 %, som er innenfor akseptable grenser.

For å rasjonalisere teknikken for å beregne belysningsstyrken ved punktmetoden, brukes romlige isolux-referansekurver konstruert for hver type lysarmaturer.