AC kondensator

La oss sette sammen kretsen med kondensator, hvor dynamoen genererer en sinusformet spenning. La oss analysere sekvensielt hva som vil skje i kretsen når vi lukker bryteren. Vi vil vurdere det første øyeblikket når generatorspenningen er lik null.

I løpet av første kvartal av perioden vil spenningen over generatorterminalene øke, fra null, og kondensatoren begynner å lades. En strøm vil vises i kretsen, men i det første øyeblikket av å lade kondensatoren, til tross for at spenningen på platene nettopp har dukket opp og fortsatt er veldig liten, vil strømmen i kretsen (ladestrømmen) være størst . Når ladningen på kondensatoren øker, avtar strømmen i kretsen og når null i det øyeblikket kondensatoren er fulladet. I dette tilfellet blir spenningen på kondensatorplatene, strengt etter spenningen til generatoren, i dette øyeblikk maksimal, men med motsatt fortegn, det vil si at den er rettet mot spenningen til generatoren.

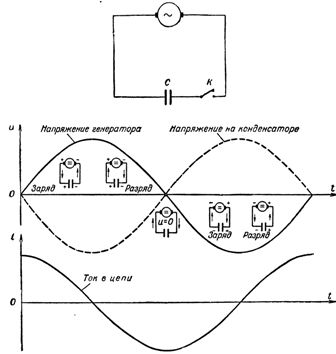
Ris. 1. Endring av strøm og spenning i en krets med kapasitans

På denne måten suser strømmen med den største kraften inn i en kondensator gratis, men begynner umiddelbart å avta når platene til kondensatoren er fylt med ladninger og faller til null, og lader den helt opp.

La oss sammenligne dette fenomenet med det som skjer med vannstrømmen i et rør som forbinder to kommuniserende kar (fig. 2), hvorav det ene er fullt og det andre tomt. Man trenger bare å trykke på ventilen som blokkerer vannveien, da vann umiddelbart strømmer fra venstre kar under stort trykk gjennom røret inn i det tomme høyre karet. Umiddelbart vil imidlertid vanntrykket i røret gradvis begynne å svekkes på grunn av utjevningen av nivåene i karene og falle til null. Vannstrømmen vil stoppe.

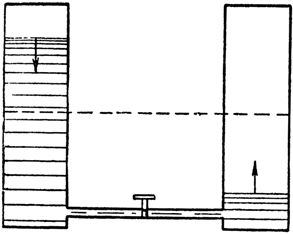
Ris. 2. Endringen i vanntrykk i røret som forbinder kommunikasjonsbeholderne er lik endringen i strøm i kretsen under ladingen av kondensatoren

På samme måte suser strømmen først inn i en uladet kondensator og svekkes deretter gradvis mens den lades.

Når det andre kvartalet av perioden begynner, når generatorspenningen først starter sakte og deretter avtar mer og raskere, vil den ladede kondensatoren lades ut til generatoren, noe som forårsaker en utladningsstrøm i kretsen. Når generatorspenningen synker, utlades kondensatoren mer og mer og utladningsstrømmen i kretsen øker. Retningen til utladningsstrømmen i dette kvartalet av perioden er motsatt av retningen til ladestrømmen i første kvartal av perioden. Følgelig er strømkurven som har passert nullverdien nå plassert under tidsaksen.

Ved slutten av den første halvsyklusen nærmer generatorspenningen, så vel som kondensatorspenningen, seg raskt null og kretsstrømmen når sakte sin maksimale verdi. Gitt at verdien av strømmen i kretsen er større, jo større verdien av ladningen som bæres i kretsen, vil det bli klart hvorfor strømmen når sitt maksimum når spenningen på platene til kondensatoren, og derfor ladningen på kondensator, avtar raskt.

Med begynnelsen av tredje kvartal av perioden begynner kondensatoren å lade opp igjen, men polariteten til platene, så vel som polariteten til generatoren, endres "og omvendt, og strømmen fortsetter å flyte i det samme retning, begynner å avta når kondensatoren lades. slutten av tredje kvartal av perioden, når generator- og kondensatorspenningene når sitt maksimum, går strømmen til null.

I løpet av det siste kvartalet av perioden faller spenningen, avtagende, til null, og strømmen, etter å ha endret retning i kretsen, når sin maksimale verdi. Her slutter perioden, hvoretter den neste begynner, nøyaktig gjentakelse av den forrige, og så videre.

Således, under påvirkning av vekselspenningen til generatoren, lades kondensatoren to ganger i løpet av perioden (det første og tredje kvartalet av perioden) og utlades to ganger (det andre og fjerde kvartalet av perioden). Men siden de veksler en etter en kondensatorladinger og -utladninger ledsaget hver gang av passering av lade- og utladningsstrømmen gjennom kretsen, kan vi konkludere med at vekselstrøm.

Du kan sjekke dette i følgende enkle eksperiment. Koble en 4-6 mikrofarad kondensator til strømnettet via en 25 W lyspære.Lyset vil tennes og vil ikke slukke før kretsen er brutt. Dette tyder på at det har gått en vekselstrøm gjennom kretsen med kapasitansen. Selvfølgelig passerer den ikke gjennom kondensatorens dielektrikum, men representerer til enhver tid enten en ladestrøm eller en kondensatorutladningsstrøm.

Som vi vet, er dielektrikumet polarisert under påvirkning av et elektrisk felt som oppstår i det når kondensatoren lades, og polarisasjonen forsvinner når kondensatoren utlades.

I dette tilfellet tjener dielektrikumet med forskyvningsstrømmen som oppstår i den for vekselstrømmen som en slags fortsettelse av kretsen, og for konstanten bryter den kretsen. Men forskyvningsstrømmen dannes bare innenfor dielektrikumet til kondensatoren, og derfor skjer ikke overføring av ladninger langs kretsen.

Motstanden som tilbys av en AC-kondensator avhenger av verdien av kondensatorens kapasitans og frekvensen til strømmen.

Jo større kapasiteten til kondensatoren er, desto større blir ladningen på kretsen under lading og utlading av kondensatoren, og følgelig jo større er strømmen i kretsen. En økning i strømmen i kretsen indikerer at motstanden er redusert.

Derfor, når kapasitansen øker, reduseres motstanden til kretsen mot vekselstrøm.

Det vokser gjeldende frekvens øker mengden ladning som bæres i kretsen fordi ladningen (så vel som utladningen) av kondensatoren må skje raskere enn ved lav frekvens. Samtidig tilsvarer en økning i mengden overført ladning per tidsenhet en økning i strømmen i kretsen og derfor en reduksjon i motstanden.

Hvis vi på en eller annen måte gradvis reduserer frekvensen til vekselstrømmen og reduserer strømmen til likestrøm, vil motstanden til kondensatoren som er inkludert i kretsen gradvis øke og bli uendelig stor (bryte kretsen) til den dukker opp i konstant strømkrets.

Derfor, når frekvensen øker, reduseres motstanden til kondensatoren mot vekselstrøm.

Akkurat som motstanden til en spole til en vekselstrøm kalles induktiv, kalles motstanden til en kondensator kapasitiv.

Derfor er den kapasitive motstanden større, jo lavere kapasiteten til kretsen er og frekvensen til strømmen som mater den.

Kapasitiv motstand er betegnet som Xc og måles i ohm.

Avhengigheten av den kapasitive motstanden av frekvensen til strømmen og kapasiteten til kretsen bestemmes av formelen Xc = 1 /ωC, hvor ω er en sirkulær frekvens lik produktet av 2πe, C er kapasiteten til kretsen i farads.

Kapasitiv motstand, som induktiv motstand, har en reaktiv natur, siden kondensatoren ikke forbruker energien til strømkilden.

formel Ohms lov for en kapasitiv krets har den formen I = U / Xc, hvor I og U - effektive verdier for strøm og spenning; Xc er den kapasitive motstanden til kretsen.

Egenskapen til kondensatorer for å gi høy motstand mot lavfrekvente strømmer og enkelt passere høyfrekvente strømmer er mye brukt i kommunikasjonsutstyrskretser.

Ved hjelp av kondensatorer oppnås for eksempel separasjon av konstante strømmer og lavfrekvente strømmer fra høyfrekvente strømmer, nødvendige for driften av kretsene.

Hvis det er nødvendig å blokkere banen til lavfrekvent strøm i høyfrekvente delen av kretsen, kobles en liten kondensator i serie. Den gir stor motstand mot lavfrekvent strøm og passerer samtidig enkelt høyfrekvent strøm.

Hvis det er nødvendig å forhindre høyfrekvent strøm, for eksempel i strømkretsen til radiostasjonen, brukes en kondensator med stor kapasitet, koblet parallelt med strømkilden. I dette tilfellet går høyfrekvente strømmen gjennom kondensatoren og omgår strømforsyningskretsen til radiostasjonen.

Aktiv motstand og kondensator i AC-kretsen

I praksis blir tilfeller ofte observert når de er i en seriekrets med en kapasitans aktiv motstand er inkludert. Den totale motstanden til kretsen i dette tilfellet bestemmes av formelen

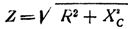
Derfor er den totale motstanden til en krets bestående av aktiv og kapasitiv AC-motstand lik kvadratroten av summen av kvadratene av den aktive og kapasitive motstanden til denne kretsen.

Ohms lov forblir gyldig for denne I = U / Z-kretsen også.

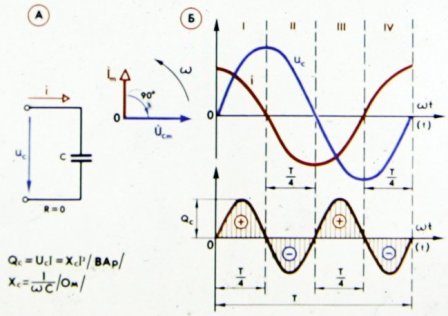
I fig. 3 viser kurvene som karakteriserer faseforholdet mellom strøm og spenning i en krets som inneholder kapasitiv og aktiv motstand.

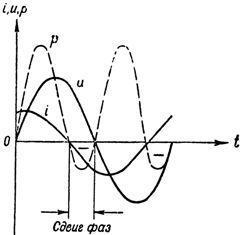
Ris. 3. Strøm, spenning og effekt i en krets med en kondensator og en aktiv motstand

Som det fremgår av figuren, øker strømmen i dette tilfellet spenningen ikke med en fjerdedel av en periode, men med mindre, siden den aktive motstanden bryter med den rent kapasitive (reaktive) naturen til kretsen, som bevist av den reduserte fasen skifte. Nå er spenningen ved kretsterminalene definert som summen av to komponenter: den reaktive komponenten til spenningen vil overvinne den kapasitive motstanden til kretsen og den aktive komponenten til spenningen, og overvinne dens aktive motstand.

Jo større den aktive motstanden til kretsen er, jo mindre faseforskyvning mellom strøm og spenning.

Kurven av effektendringen i kretsen (se fig. 3) to ganger i løpet av perioden fikk et negativt fortegn, som, som vi allerede vet, er en konsekvens av kretsens reaktive natur. Jo mindre reaktiv kretsen er, desto mindre faseforskyvning mellom strøm og spenning, og jo mer strøm kildestrøm bruker den kretsen.

Les også: Spenningsresonans