Hva er en elektrisk forsyning?

Det moderne mennesket møter konstant elektrisitet i hverdagen og på jobben, bruker enheter som forbruker elektrisk strøm og enheter som genererer den. Når du arbeider med dem, bør du alltid ta hensyn til deres evner som ligger i de tekniske egenskapene.

En av hovedindikatorene for enhver elektrisk enhet er en slik fysisk mengde som elektrisk energi... Det er vanlig å kalle intensiteten eller hastigheten på generering, overføring eller konvertering av elektrisitet til andre typer energi, for eksempel varme, lys, mekanisk.

Transport eller overføring av stor elektrisk energi til industrielle formål utføres iht høyspentledninger.

Transformasjon elektrisk energi utføres ved transformatorstasjoner.

Elektrisitetsforbruk forekommer i husholdnings- og industriapparater til ulike formål. En av deres vanlige typer er glødelamper av forskjellige karakterer.

Den elektriske kraften til generatorer, kraftledninger og forbrukere i DC- og AC-kretser har samme fysiske betydning, som samtidig uttrykkes i forskjellige forhold avhengig av formen på de sammensatte signalene. For å definere de generelle mønstrene, forestillinger om øyeblikkelige verdier... De understreker igjen avhengigheten av hastigheten på transformasjon av elektrisitet på tid.

Bestemmelse av øyeblikkelig elektrisk kraft

I teoretisk elektroteknikk, for å utlede de grunnleggende forholdene mellom strøm, spenning og kraft, brukes bildene deres i form av øyeblikkelige verdier, som er faste på et bestemt tidspunkt.

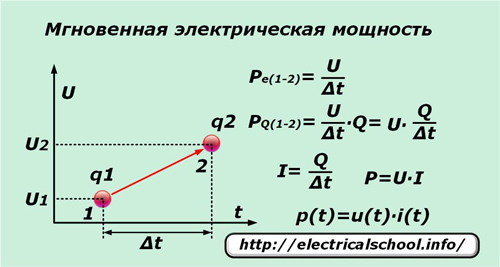
Hvis i løpet av en veldig kort periode ∆t en enkelt elementær ladning q under påvirkning av spenning U beveger seg fra punkt «1» til punkt «2», så utfører den arbeid lik potensialforskjellen mellom disse punktene. Ved å dele det på tidsintervallet ∆t får vi uttrykket for den øyeblikkelige effekten per ladningsenhet Pe (1-2).

Siden ikke bare den ene ladningen beveger seg under påvirkning av den påførte spenningen, men også alle de tilstøtende som er under påvirkning av denne kraften, hvis nummer er praktisk representert av tallet Q, så den øyeblikkelige verdien av kraften PQ (1-2) kan skrives for dem.

Etter å ha utført enkle transformasjoner, får vi uttrykket for kraften P og avhengigheten av dens øyeblikkelige verdi p (t) av komponentene i produktet av den øyeblikkelige strømmen i (t) og spenningen u (t).

Bestemmelse av konstant elektrisk effekt

V DC-kretser størrelsen på spenningsfallet i kretsseksjonen og strømmen som strømmer gjennom den endres ikke og forblir stabil, lik de øyeblikkelige verdiene.Derfor kan kraften i denne kretsen bestemmes ved å multiplisere disse verdiene eller dividere det perfekte arbeidet A med utførelsesperioden, som vist i det forklarende bildet.

Bestemmelse av elektrisk vekselstrøm

Lovene for sinusformet variasjon av strømmer og spenninger overført gjennom elektriske nettverk pålegger deres innflytelse på uttrykket av kraft i slike kretser. Her spiller tilsynelatende kraft inn, som beskrives av krafttrekanten og består av aktive og reaktive komponenter.

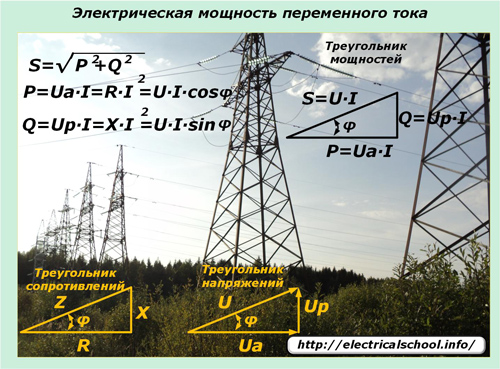
En sinusformet elektrisk strøm når den passerer gjennom kraftledninger med blandede typer belastninger i alle seksjoner, endrer ikke formen på dens harmoniske. Og spenningsfallet ved reaktive belastninger skifter i fase i en bestemt retning. Momentverdiuttrykk hjelper til med å forstå effekten av påførte belastninger på effektendringen i kretsen og dens retning.

Vær samtidig oppmerksom på det faktum at retningen til strømstrømmen fra generatoren til forbrukeren og den overførte kraften gjennom den opprettede kretsen er helt forskjellige ting, som i noen tilfeller ikke bare kan falle sammen, men også være rettet i motsatte retninger.

Tenk på disse forholdene i deres ideelle, rene manifestasjon for forskjellige typer belastninger:

• aktiv;

• kapasitiv;

• induktiv.

Aktiv lasteffekttap

Vi vil anta at generatoren produserer en ideell sinusformet spenning u som påføres den rent aktive motstanden til kretsen. Amperemeter A og voltmeter V måler strøm I og spenning U hver gang t.

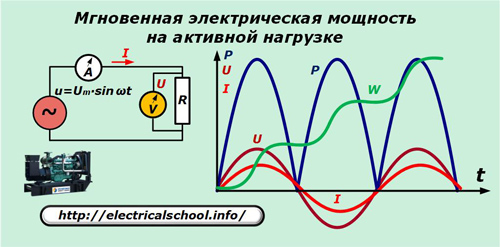
Grafen viser at sinusformene til strømmen og spenningsfallet over den aktive motstanden samsvarer i frekvens og fase, og gir de samme svingningene. Kraften uttrykt av produktet deres svinger med to ganger frekvensen og forblir alltid positiv.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Hvis vi går til uttrykket driftsspenning, da får vi: p = P ∙ (1-cos2ωt).

Vi vil da integrere kraften over perioden av en svingning T og vi vil kunne merke at energiforsterkningen ∆W i løpet av dette intervallet øker. Over tid fortsetter motstanden å forbruke nye deler av elektrisitet, som vist i grafen.

Med reaktive belastninger er egenskapene til energiforbruk forskjellige, de har en annen form.

Kapasitiv effekttap

I den elektriske kretsen til generatoren, bytt ut det resistive elementet med en kondensator med kapasitans C.

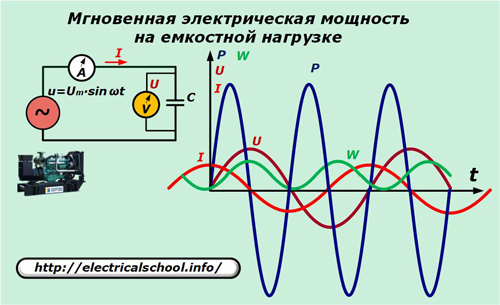
Forholdet mellom strømmen og spenningsfallet i kapasitansen uttrykkes ved forholdet: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Vi multipliserer verdiene til de øyeblikkelige uttrykkene for strøm med spenning og får verdien av kraften som forbrukes av den kapasitive lasten.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt sin = U2) ∙ t sin = U2/ (2X.

Her kan du se at effekten svinger rundt null ved to ganger frekvensen av den påførte spenningen. Dens totale verdi for den harmoniske perioden, så vel som energiforsterkningen, er null.

Dette betyr at energi beveger seg langs den lukkede kretsen til kretsen i begge retninger, men ikke virker.Et slikt faktum forklares av det faktum at når kildespenningen øker i absolutt verdi, er effekten positiv, og energistrømmen gjennom kretsen ledes til beholderen, hvor energi akkumuleres.

Etter at spenningen går til den fallende harmoniske seksjonen, returneres energi fra kondensatoren til kretsen til kilden. Det gjøres ikke noe nyttig arbeid i noen av prosessene.

Effekttap i en induktiv last

Nå, i forsyningskretsen, bytt ut kondensatoren med induktans L.

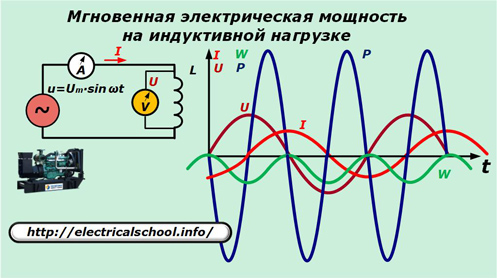
Her er strømmen gjennom induktansen uttrykt ved forholdet:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Så får vi

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sinω2ωt (2ХL) ∙ t sinω2ωt (2).

De resulterende uttrykkene lar oss se arten av endringen i kraftens retning og økningen av energi på induktansen, som utfører de samme svingningene som er ubrukelige for å utføre arbeid, som på kapasitansen.

Effekten som frigjøres i reaktive belastninger kalles reaktiv komponent. Under ideelle forhold, når tilkoblingsledningene ikke har noen aktiv motstand, virker det ufarlig og forårsaker ingen skade. Men under reelle strømforhold forårsaker periodiske transienter og reaktive effektsvingninger oppvarming av alle aktive elementer, inkludert tilkoblingsledninger, for hvilke noe energi forbrukes og verdien av den påførte fulle kraften til kilden reduseres.

Hovedforskjellen mellom den reaktive komponenten av kraft er at den ikke utfører nyttig arbeid i det hele tatt, men fører til tap av elektrisk energi og overflødig belastning på utstyr, som er spesielt farlig i kritiske situasjoner.

Av disse grunner, for å eliminere påvirkningen av reaktiv kraft, esp tekniske systemer for kompensasjon.

Kraftfordeling ved blandet belastning

Som et eksempel bruker vi belastningen til en generator med en aktiv kapasitiv karakteristikk.

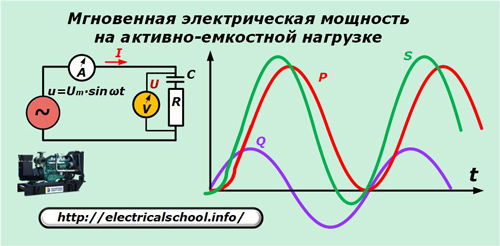
For å forenkle bildet er ikke sinusoidene til strømmer og spenninger vist i den gitte grafen, men det bør tas i betraktning at med en aktiv-kapasitiv karakter av lasten, leder strømvektoren spenningen.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Etter transformasjoner får vi: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Disse to begrepene i det siste uttrykket er de aktive og reaktive komponentene til den øyeblikkelige tilsynelatende kraften. Bare den første av disse gjør nyttig arbeid.

Verktøy for kraftmåling

For å analysere forbruket av elektrisitet og beregne for det, brukes måleapparater, som lenge har blitt kalt «Tellere»… Arbeidet deres er basert på å måle de effektive verdiene for strøm og spenning og automatisk multiplisere dem med en utgang av informasjon.

Målere viser energiforbruk ved å telle driftstiden til elektriske apparater på en inkrementell basis fra det øyeblikket måleren slås på under belastning.

For å måle den aktive komponenten av strøm i AC-kretser, wattmålere, og reaktive - varmetere. De har forskjellige enhetsbetegnelser:

• watt (W, W);

• var (var, var, var).

For å bestemme det totale energiforbruket, er det nødvendig å beregne verdien ved hjelp av krafttrekantformelen basert på avlesningene til wattmeteret og varmeteret. Det uttrykkes i sine egne enheter - volt-ampere.

De aksepterte betegnelsene på enhetene til hver hjelper elektrikere til å bedømme ikke bare verdien, men også arten av kraftkomponenten.