RMS-verdier for strøm og spenning

Den sinusformede vekselstrømmen har forskjellige øyeblikksverdier i løpet av perioden. Det er naturlig å stille spørsmålet, hvilken verdi av strøm vil bli målt med amperemeteret inkludert i kretsen?

Ved beregning av vekselstrømkretser, så vel som elektriske målinger, er det upraktisk å bruke øyeblikkelige eller amplitudeverdier av strømmer og spenninger, og deres gjennomsnittsverdier over en periode er null. I tillegg kan den elektriske effekten av en periodisk skiftende strøm (mengden av frigjort varme, perfekt drift, etc.) ikke estimeres ved amplituden til denne strømmen.

Det mest praktiske var introduksjonen av konseptene for de såkalte effektive verdiene for strøm og spenning... Disse konseptene er basert på den termiske (eller mekaniske) virkningen av strømmen, som ikke avhenger av retningen.

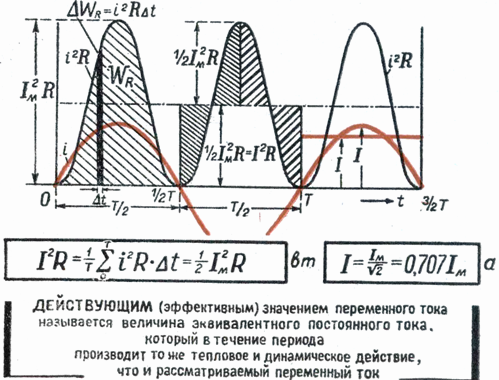
Root mean square verdi av vekselstrøm - dette er verdien av likestrøm som i løpet av perioden med vekselstrøm frigjøres samme mengde varme i lederen som under vekselstrøm.

For å evaluere handlingene som er utført vekselstrøm, vil vi sammenligne dens handlinger med den termiske effekten av likestrøm.

Likestrøm P A som går gjennom motstand r vil være P = P2r.

Vekselstrøm uttrykkes som den gjennomsnittlige effekten av den øyeblikkelige effekten Az2r over hele perioden eller gjennomsnittet av (jeg er x sinωT)2 NS r for samme tid.

La gjennomsnittsverdien av t2 for perioden være M. Ved å sette likhetstegn mellom kraften til likestrøm og effekten av vekselstrøm har vi: Az2r = Mr -n, hvorav Az = √M,

Mengden I kalles den effektive verdien av vekselstrømmen.

Gjennomsnittsverdien av i2 ved vekselstrøm bestemmes som følger.

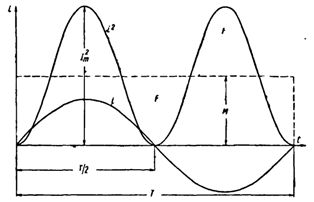
La oss konstruere en sinusformet strømkurve. Ved å kvadrere hver øyeblikkelig strømverdi får vi en P versus tid-kurve.

AC rms verdi

Begge halvdelene av denne kurven ligger over den horisontale aksen, siden de negative strømmene (-i) i andre halvdel av perioden, i kvadrat gir positive verdier.

Konstruer et rektangel med basis T og areal lik arealet avgrenset av kurven i2 og horisontal akse. Høyden på rektangelet M vil tilsvare gjennomsnittsverdien av P for perioden. Denne periodeverdien, beregnet ved bruk av høyere matematikk, vil være lik 1/2 I2m... Derfor er M. = 1/2 I2m

Siden rms-verdien Im vekselstrøm er Im = √M, så til slutt I = Im / √2

På samme måte har forholdet mellom rms og amplitudeverdiene for spenningen U og E formen:

U = Um / √2E = Em / √2

De effektive verdiene til variablene er indikert med store bokstaver uten tegninger (I, U, E).

Basert på ovenstående kan vi si at den effektive verdien av en vekselstrøm er lik en slik likestrøm, som, som passerer gjennom samme motstand som vekselstrømmen, frigjør samme mengde energi på samme tid.

Elektriske måleinstrumenter (amperemeter, voltmeter) inkludert i en vekselstrømkrets indikerer de effektive verdiene for strøm eller spenning.

Når du konstruerer vektordiagrammer, er det mer praktisk å utsette ikke amplituden, men de effektive verdiene til vektorene. For dette reduseres lengdene til vektorene med √2 én gang. Dette endrer ikke plasseringen av vektorene på diagrammet.