Logiske enheter

Logisk algebra eller boolsk algebra brukes til å beskrive virkeloven til digitale kretser. Logikkens algebra er basert på konseptet om en "hendelse" som kanskje eller ikke kan skje. En hendelse som har skjedd regnes som sann og et logisk nivå «1» er uttrykt, en hendelse som ikke har skjedd regnes som usann og et logisk nivå «0» er uttrykt.

Hendelsen påvirkes av variabler og de påvirker i henhold til en viss lov. Denne loven kalles en logisk funksjon, variablene er argumenter... Che. den logiske funksjonen er funksjonen y = f (x1, x2, … xn), som tar verdiene «0» eller «1». Variablene x1, x2, … xn har også verdiene «0» eller «1».

Algebra of logic - en gren av matematisk logikk som studerer strukturen til komplekse logiske utsagn og måter å etablere deres sannhet ved algebraiske metoder. I formlene for logisk algebra er variablene logiske eller binære, det vil si at de bare tar to verdier - usann og sann, som er betegnet med henholdsvis 0 og 1. Hvert dataprogram inneholder logiske operasjoner.

Enheter designet for å danne funksjoner til den logiske algebraen kalles logiske enheter... En logisk enhet har et hvilket som helst antall innganger og bare én utgang (fig. 1).

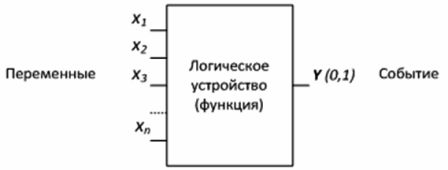
Figur 1 — Logisk enhet

For eksempel inkluderer en elektronisk kombinasjonslås en logisk enhet for hvilken hendelse (y) er åpningen av låsen. For at hendelsen (y = 1) skal inntreffe, dvs. låsen har åpnet, er det nødvendig å definere variablene — ti knapper på det numeriske tastaturet. Visse knapper må trykkes inn, dvs. ta verdien «1» og trykk samtidig i en bestemt rekkefølge — en logisk funksjon.

Det er praktisk å representere enhver logisk funksjon i form av en tilstandstabell (sannhetstabell), der mulige kombinasjoner av variabler (argumenter) og den tilsvarende verdien av funksjonen er registrert.

Logiske enheter er bygget på logiske porter som utfører en bestemt funksjon. De grunnleggende logiske funksjonene er logisk addisjon, logisk multiplikasjon og logisk negasjon.

1) ELLER (ELLER) — logisk addisjon eller divisjon (fra engelsk disjunksjon — avbrudd) — en logisk enhet vises ved utgangen av dette elementet når en enhet vises ved minst én av inngangene. Utgangen vil kun være logisk null når det er et logisk nullsignal på alle innganger.

Denne operasjonen kan utføres ved å bruke en kontaktkrets med to kontakter koblet parallelt. «1» ved utgangen til en slik krets vil vises hvis minst en av kontaktene er lukket.

2) OG (AND) — logisk multiplikasjon eller forbindelse (fra den engelske unionen — forbindelse, & — og-tegnet) — ved utgangen av dette elementet vises signalet til en logisk enhet bare når en logisk enhet er til stede ved alle innganger.Hvis minst én inngang er null, vil utgangen også være null.

Denne operasjonen kan utføres av en kontaktkrets som består av kontakter koblet i serie.

3) IKKE – logisk negasjon eller inversjon indikert med en strek over en variabel – operasjonen utføres på én variabel x og verdien av y er det motsatte av den variabelen.

Operasjonen kan IKKE utføres med en normalt lukket kontakt på det elektromagnetiske reléet: det er ingen spenning på reléspolen (x = 0) — kontakten er også lukket på utgangen «1» (y = 1). Ved tilstedeværelse av spenning på reléspolen (x = 1), er kontakten også åpen på «0»-utgangen (y = 0).

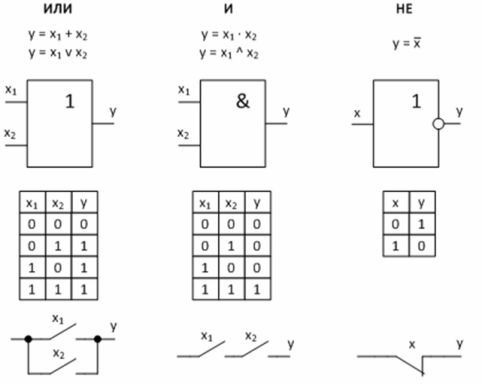
Figur 2 — Grunnleggende logiske funksjoner og deres implementering

Logiske enheter bruker forskjellige logiske porter. Spesielt viktig er to universelle logiske operasjoner, som hver er i stand til uavhengig å danne enhver logisk funksjon.

4) NAND — Schäfer-funksjon.

5) ELLER IKKE — Punch-funksjon.

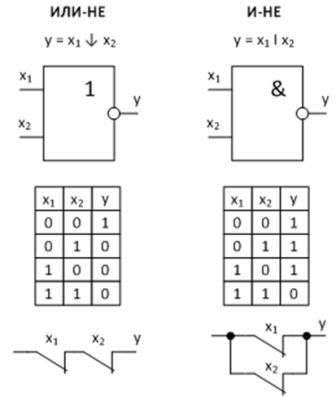
Figur 3 — Universelle logiske funksjoner og deres implementering

Eksempel: Sikkerhetsalarmkrets basert på logiske elementer. Generator G genererer et sirenesignal som mater det til forsterkertrinnet gjennom det logiske elementet «AND» på mikrokretsen DD2. Når beskyttelsesbryterne S1 — S4 er lukket, virker nivået «0» på inngangene til elementet DD1 — nivået «0» er på den nedre inngangen til elementet «I» DD2, som betyr at porten til transistoren VT er også «0».

I tilfelle av å åpne minst en av bryterne, for eksempel S1, vil inngangen til elementet DD1 gjennom motstanden R1 motta en spenning på nivå «1», noe som vil føre til utseendet til «1» ved den andre inngangen til elementet «OG» DD1.Dette vil tillate signalet fra generatoren G å passere til porten til transistoren hvis belastning er høyttaleren.

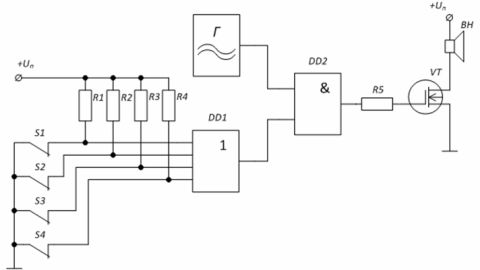
Figur 4 — Alarmbeskyttelsesskjema

Komplekse digitale kretser bygges ved å gjenta grunnleggende logiske kretser om og om igjen. Verktøyet for slik konstruksjon er boolsk algebra, som med tanke på digital teknologi kalles logisk algebra. I motsetning til en variabel i vanlig algebra, har en boolsk variabel bare to verdier, som kalles boolsk null og boolsk en.

Logisk null og logisk en er betegnet med 0 og 1. I logisk algebra er 0 og 1 ikke tall, men logiske variabler. I logisk algebra er det tre grunnleggende operasjoner mellom logiske variabler: logisk multiplikasjon (konjunksjon), logisk addisjon (disjunksjon) og logisk negasjon (inversjon).

Elektroniske kretser som utfører den samme logiske funksjonen, men satt sammen med forskjellige elementer, forskjellig i strømforbruk, forsyningsspenning, verdier for høye og lave utgangsspenningsnivåer, signalutbredelsesforsinkelsestid og lastbærende kapasitet.

Se også om dette emnet: AND, OR, NOT, AND-NOT, OR-NOT logiske porter og deres sannhetstabeller