Bestemmelse av motoreffekt under repeterende transient drift
 Driftsmåten til den elektriske stasjonen, der driftsperiodene er av en slik varighet, og veksler med pauser av en viss varighet, at temperaturen på alle enhetene som utgjør den elektriske stasjonen ikke når en stabil verdi, verken i hver arbeidsperiode eller i hver pause kalles avbrudd.
Driftsmåten til den elektriske stasjonen, der driftsperiodene er av en slik varighet, og veksler med pauser av en viss varighet, at temperaturen på alle enhetene som utgjør den elektriske stasjonen ikke når en stabil verdi, verken i hver arbeidsperiode eller i hver pause kalles avbrudd.
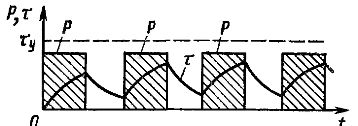
Det periodiske belastningsregimet tilsvarer grafer som ligner de som er vist i fig. 1. Overopphetingen av den elektriske motoren varierer langs den stiplede linjen til en sag som består av vekslende segmenter av varme- og kjølekurver. Intermitterende belastningsmodus er typisk for de fleste verktøymaskiner.
Ris. 1. Intermitterende belastningsplan
Kraften til en elektrisk motor som opererer i periodisk modus bestemmes mest hensiktsmessig av formelen for gjennomsnittlige tap, som kan skrives som
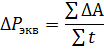
hvor ΔA er energitapet ved hver belastningsverdi, inkludert start- og stoppprosessen.
Når den elektriske motoren ikke fungerer, forverres kjøleforholdene betydelig. Dette tas hensyn til ved å innføre eksperimentelle koeffisienter β0 <1. Pausetiden t0 multipliseres med koeffisienten β0, som et resultat av at nevneren til formelen reduseres, og de ekvivalente tapene ΔREKV øker, og følgelig øker den nominelle effekten til den elektriske motoren.
For asynkronbeskyttede motorer i A-serien med en synkron hastighet på 1500 rpm og en effekt på 1-100 kW, er β0-koeffisienten 0,50-0,17, og for nedblåsningsmotorer β0 = 0,45-0,3 (med en økning i Пн , koeffisient β0 synker). For lukkede motorer er β0 nær enhet (0,93-0,98). Dette er fordi ventilasjonseffektiviteten til lukkede motorer er lav.
Ved start og stopp er gjennomsnittshastigheten til den elektriske motoren lavere enn den nominelle, som et resultat av at kjølingen av den elektriske motoren også forringes, som er preget av koeffisienten

Ved bestemmelse av koeffisienten β1 er det betinget antatt at endringen i rotasjonsfrekvensen skjer etter en lineær lov og at koeffisienten β1 lineært avhenger av denne.
Når vi kjenner koeffisientene β0 og β1, får vi
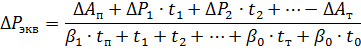
hvor ΔР1, ΔР2, — effekttap ved forskjellige belastninger, kW; t1 t2 — handlingstid for disse lastene, s; tn, tT, t0 — start-, forsinkelses- og pausetid, s; ΔАп ΔАТ — energitap i motoren under start og stopp, kJ.
Som nevnt ovenfor, må hver motor velges for varme- og overbelastningsforhold. For å bruke metoden for gjennomsnittlige tap, er det nødvendig å sette opp en viss elektrisk motor på forhånd, som i dette tilfellet også anbefales å velges i henhold til overbelastningsforholdene.Den ekvivalente kraftformelen kan brukes for en grov beregning i tilfeller der start og stopp er sjeldne og ikke påvirker oppvarmingen av den elektriske motoren nevneverdig.
I maskinteknikk, for drift i intermitterende belastningsmodus, brukes elektriske motorer designet for å operere med en kontinuerlig belastning. Elektroindustrien produserer også motorer spesialdesignet for å håndtere intermitterende belastninger, som er mye brukt i løfte- og transportkonstruksjoner. Slike elektriske motorer velges under hensyntagen til den relative varigheten av inkludering:

hvor tp er motorens gangtid; t0 — pausevarighet.
Et eksempel på valg av motor med kraft i multippel korttidsdriftsmodus.
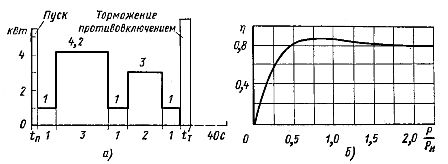
Bestem kraften til den elektriske motoren ved n0 - 1500 rpm; motoren fungerer i henhold til belastningsplanen vist i fig. 2, a. Elektrisk motorakseleffekt ved tomgang Pxx = 1 kW. Redusert treghetsmoment for maskinen Jc = 0,045 kg-m2.
Svar:
1. Forhåndsvelg den elektriske motoren i henhold til overbelastningsforholdene, slik som λ = 1,6:

I henhold til katalogen velger vi en elektrisk motor med den beskyttede versjonen av nærmeste høyeffekt (2,8 kW), der mon = 1420 rpm;

For denne motoren λ = 0,85 • 2 = 1,7. På denne måten velges motoren med en viss overbelastningsgrense.
Avhengigheten η = f (P / Pн) til denne motoren er vist i fig. 2, b.
Ris. 2. Avhengigheter N = f (t) og η = f (P / Pн)
2. I henhold til formelen
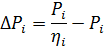
vi oppdager tap ved potenser 1; 3; 4,2 kW (på skjema). Tapene er henholdsvis 0,35; 0,65 og 1 kW. Vi finner tap ved Pn = 2,8 kW, som er ΔPn = 0,57 kW.
3. Bestem starttidspunkt og stopptid ved motstand:
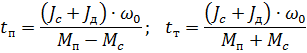
hvor:
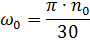
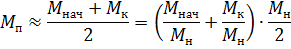



Vi får tn = 0,30 s; tt = 0,21 s.
4. Bestem start- og stopptapene:

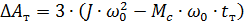
Vi får ΔAp = 1,8 kJ og ΔAt = 3,8 kJ.
5. Finn tilsvarende tap i loopen:
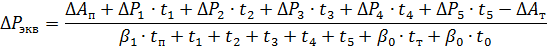
hvor
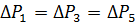
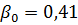
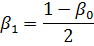
Vi får ΔREKV = 0,44 kW. Siden ΔPn = 0,57, er ΔREKV <ΔPn og derfor motoren riktig valgt.