Spenningsresonans
Hvis AC-kretsen er koblet i serie induktor og kondensator, så påvirker de på hver sin måte generatoren som mater kretsen og faseforbindelsene mellom strøm og spenning.
En induktor introduserer en faseforskyvning der strømmen henger etter spenningen med en kvart periode, mens en kondensator tvert imot gjør at spenningen i kretsen ettersetter strømmen med en kvart periode. Dermed er effekten av induktiv motstand på faseforskyvningen mellom strøm og spenning i en krets motsatt av effekten av kapasitiv motstand.
Dette fører til at den totale faseforskyvningen mellom strøm og spenning i kretsen avhenger av forholdet mellom de induktive og kapasitive motstandsverdiene.
Hvis verdien av den kapasitive motstanden til kretsen er større enn den induktive, er kretsen kapasitiv av natur, det vil si at spenningen henger etter strømmen i fase. Hvis tvert imot den induktive motstanden til kretsen er større enn den kapasitive, så leder spenningen strømmen og derfor er kretsen induktiv.
Den totale reaktansen Xtot til kretsen vi vurderer bestemmes ved å legge til den induktive motstanden til spolen XL og den kapasitive motstanden til kondensatoren XC.
Men siden virkningen av disse motstandene i kretsen er motsatt, blir en av dem, nemlig Xc, tildelt et minustegn, og den totale reaktansen bestemmes av formelen:
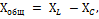
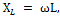
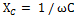
Bruk på denne kretsen Ohms lov, vi får:
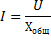
Denne formelen kan transformeres som følger:
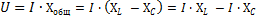
I den resulterende ligningen, AzxL - den effektive verdien av komponenten av den totale spenningen til kretsen, som vil overvinne den induktive motstanden til kretsen, og AzNSC - den effektive verdien av komponenten av den totale spenningen til kretsen, som vil overvinne den kapasitive motstanden.
Dermed kan den totale spenningen til en krets som består av en seriekobling av en spole og en kondensator betraktes som bestående av to ledd, hvis verdier avhenger av verdiene til den induktive og kapasitive motstanden til krets.
Vi trodde at en slik krets ikke har noen aktiv motstand. Imidlertid, i tilfeller der den aktive motstanden til kretsen ikke lenger er så liten at den er ubetydelig, bestemmes den totale motstanden til kretsen av følgende formel:
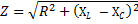
der R er den totale aktive motstanden til kretsen, XL -NSC - dens totale reaktans. Går vi til formelen til Ohms lov, har vi rett til å skrive:
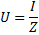
AC spenningsresonans
Induktive og kapasitive motstander koblet i serie forårsaker mindre faseforskyvning mellom strøm og spenning i en AC-krets enn om de var inkludert i kretsen separat.
Med andre ord, fra den samtidige handlingen av disse to reaksjonene av forskjellig karakter i kretsen, skjer kompensasjon (gjensidig ødeleggelse) av faseforskyvningen.
Full erstatning, dvs. fullstendig eliminering av faseforskyvningen mellom strøm og spenning i en slik krets vil skje når den induktive motstanden er lik den kapasitive motstanden til kretsen, dvs. når XL = XC eller, som er det samme, når ωL = 1 / ωC.
I dette tilfellet vil kretsen oppføre seg som en rent aktiv motstand, det vil si som om den verken har en spole eller en kondensator. Verdien av denne motstanden bestemmes av summen av de aktive motstandene til spolen og tilkoblingsledningene. Ved hvilken effektiv strøm i kretsen vil være den største og bestemmes av Ohms lovformel I = U / R hvor Z nå er erstattet av R.
Samtidig vil spenningene som virker på spolen UL = AzxL og på kondensatoren Uc = AzNSCC være like og være så store som mulig. Med lav aktiv motstand i kretsen kan disse spenningene mange ganger overstige den totale spenningen U til kretsterminalene. Dette interessante fenomenet kalles spenningsresonans i elektroteknikk.
I fig. 1 viser kurvene for spenninger, strømmer og effekt ved resonansspenninger i kretsen.
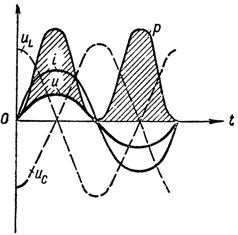
Graf over spenningsstrøm og effekt ved spenningsresonans
Det bør huskes at motstandene XL og C er variabler som avhenger av frekvensen til strømmen, og det er verdt i det minste å endre frekvensen litt, for eksempel å øke den når XL = ωL vil øke, og XSC = = 1 / ωC vil avta og dermed vil spenningsresonansen i kretsen umiddelbart bli forstyrret, mens sammen med den aktive motstanden vil reaktansen vises i kretsen. Det samme vil skje hvis du endrer verdien på induktansen eller kapasitansen til kretsen.
Med spenningsresonans vil kraften til strømkilden bare brukes for å overvinne den aktive motstanden til kretsen, det vil si å varme opp ledningene.
Faktisk, i en krets med en enkelt induktiv spole, oppstår energisvingninger, dvs. periodisk overføring av energi fra generatoren til magnetfelt spoler. I en krets med en kondensator skjer det samme, men på grunn av energien til kondensatorens elektriske felt. I en krets med en kondensator og en induktor ved spenningsresonans (ХL = XС) går energien, når den er lagret av kretsen, periodisk fra spolen til kondensatoren og omvendt, og bare energiforbruket som er nødvendig for å overvinne den aktive motstanden til kretsen faller på andelen av strømkilden. Derfor skjer energiutvekslingen mellom kondensatoren og spolen nesten uten medvirkning fra generatoren.
Man trenger bare å bryte en spenningsresonans etter verdi, hvordan energien til magnetfeltet til spolen blir ulik energien til det elektriske feltet til kondensatoren, og i prosessen med energiutveksling mellom disse feltene vil et overskudd av energi vises, som med jevne mellomrom vil strømme ut fra kilden i kretsen, og deretter mate den tilbake til den i kretsen.
Dette fenomenet er veldig likt det som skjer i et urverk. En klokkes pendel ville vært i stand til å svinge kontinuerlig uten hjelp av en fjær (eller en vekt i en klokkerullator) hvis det ikke var for friksjonskreftene som bremser dens bevegelse.
Fjæren, ved å overføre noe av energien sin til pendelen i riktig øyeblikk, hjelper den til å overvinne friksjonskreftene, og dermed oppnå kontinuitet i svingningen.
Tilsvarende, i en elektrisk krets, når det oppstår resonans i den, bruker strømkilden sin energi bare for å overvinne den aktive motstanden til kretsen, og hjelper dermed den oscillerende prosessen i den.
Dermed kommer vi frem til at en vekselstrømkrets, bestående av en generator og en seriekoblet induktor og kondensator, under visse forhold XL = XС blir et oscillerende system... Denne kretsen ble kalt en oscillerende krets.
Fra ligningen XL = XС er det mulig å bestemme verdiene for frekvensen til generatoren der fenomenet spenningsresonans oppstår:
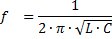
Dette betyr kapasitans og induktans til kretsen der spenningsresonans oppstår:
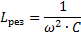
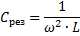
Ved å endre noen av disse tre mengdene (eres, L og C), er det mulig å forårsake spenningsresonans i kretsen, det vil si å gjøre kretsen om til en oscillerende krets.
Et eksempel på en nyttig anvendelse av spenningsresonans: Inngangskretsen til en mottaker justeres av en variabel kondensator (eller variometer) på en slik måte at spenningsresonans oppstår i den. Dette oppnår en stor økning i spolespenningen som kreves for normal mottakerdrift sammenlignet med kretsspenningen som skapes av antennen.
Sammen med nyttig bruk av fenomenet spenningsresonans i elektroteknikk, er det ofte tilfeller der spenningsresonans er skadelig En stor økning i spenningen i individuelle deler av kretsen (på spolen eller på kondensatoren) sammenlignet med spenningen av generatoren kan føre til skade på separate deler og måleenheter.

