Linearisering av sensorkarakteristikk

Linearisering av sensorkarakteristikk - en ikke-lineær transformasjon av sensorutgangsverdien eller en mengde proporsjonal med den (analog eller digital) som oppnår et lineært forhold mellom den målte verdien og verdien som representerer den.

Ved hjelp av linearisering er det mulig å oppnå linearitet på skalaen til den sekundære enheten som en sensor med en ikke-lineær karakteristikk er koblet til (f.eks. termoelement, termisk motstand, gassanalysator, strømningsmåler, etc.). Lineariseringen av sensorkarakteristikkene gjør det mulig å oppnå nødvendig målenøyaktighet gjennom sekundære enheter med digital utgang. Dette er nødvendig i noen tilfeller når sensorer kobles til opptaksenheter eller når man utfører matematiske operasjoner på den målte verdien (f.eks. integrasjon).

Når det gjelder koderkarakteristikken, fungerer lineariseringen som en invers funksjonell transformasjon.Hvis karakteristikken til sensoren er representert som y = F (a + bx), hvor x er den målte verdien, a og b er konstanter, bør karakteristikken til linearisatoren koblet i serie med sensoren (fig. 1) se ut. slik: z = kF (y), hvor F er den inverse funksjonen til F.

Som et resultat vil utgangen fra linearisatoren være z = kF(F (a + bx)) = a ' + b'x, dvs. en lineær funksjon av den målte verdien.

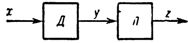
Ris. 1. Generalisert lineariseringsblokkdiagram: D - sensor, L - linearizer.

Videre, ved skalering, reduseres avhengigheten z til formen z '= mx, hvor m er den passende skaleringsfaktoren. Hvis lineariseringen gjøres på en kompenserende måte, dvs. basert på et servosystem som fig. 2, bør karakteristikken til lineariseringsfunksjonsomformeren være lik karakteristikken til sensoren z = cF (a + bx), fordi den lineariserte verdien til den målte verdien er hentet fra inngangen til omformeren til funksjonslinearisatoren og dens output sammenlignes med utgangsverdien til sensoren.

Et karakteristisk trekk ved linearisatorer som funksjonelle omformere er en relativt smal klasse av avhengigheter reprodusert av dem, begrenset til monotone funksjoner, som bestemmes av typen sensorkarakteristikk.

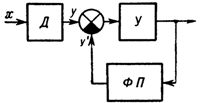
Ris. 2. Blokkdiagram over linearisering basert på sporingssystemet: D — sensor, U — forsterker (transduser), FP — funksjonell omformer.

Linearisatorer kan klassifiseres i henhold til følgende kriterier:

1. I henhold til metoden for å sette funksjonen: romlig i form av maler, matriser, etc., i form av en kombinasjon av ikke-lineære elementer, i form av en digital beregningsalgoritme, enheter.

2.Etter graden av fleksibilitet av ordningen: universell (dvs. rekonfigurerbar) og spesialisert.

3. Av arten av strukturdiagrammet: åpen (fig. 1) og kompensasjon (fig. 2) type.

4. I form av inngangs- og utgangsverdier: analog, digital, blandet (analog-digital og digital-analog).

5. Etter type elementer som brukes i kretsen: mekaniske, elektromekaniske, magnetiske, elektroniske, etc.

Romlige funksjonslinearisatorer inkluderer først og fremst kammekanismer, mønstre og ikke-lineære potensiometre. De brukes i tilfeller der den målte verdien av hvert konverteringstrinn presenteres i form av mekanisk bevegelse (kammene - for linearisering av egenskapene til manometriske sensorer og transformatorsensorer, modeller - i opptakere, ikke-lineære potensiometre - i potensial- og brokretser ).

Ulineariteten til potensiometerkarakteristikkene oppnås ved å vikle på profilerte rammer og seksjonere ved å bruke den stykkevise lineære tilnærmingsmetoden ved å manøvrere seksjonene med passende motstand.

I en linearisator basert på et elektromekanisk servosystem av potensiometrisk type som bruker et ikke-lineært potensiometer (fig. 3), vises den lineariserte verdien som en rotasjonsvinkel eller mekanisk forskyvning. Disse linearisatorene er enkle, allsidige og mye brukt i sentraliserte kontrollsystemer.

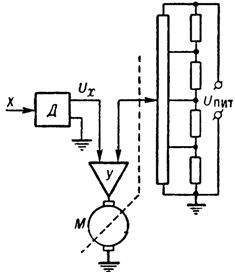
Ris. 3. Linearizer for elektromekanisk servosystem av potensiometrisk type: D — sensor med utgang i form av likespenning, Y — forsterker, M — elektrisk motor.

Ikke-lineariteter av egenskapene til individuelle elementer (elektroniske, magnetiske, termiske, etc.) brukes i parametriske funksjonelle omformere. Men mellom de funksjonelle avhengighetene de utvikler og egenskapene til sensorene, er det vanligvis ikke mulig å oppnå en fullstendig match.

Den algoritmiske måten å sette en funksjon på brukes i digitale funksjonsomformere. Deres fordeler er høy nøyaktighet og stabilitet av egenskaper. De bruker de matematiske egenskapene til individuelle funksjonelle avhengigheter eller prinsippet om lineær tilnærming etter deler. For eksempel utvikles en parabel basert på egenskapene til kvadrater av heltall.

For eksempel er en digital linearizer basert på den stykkevise lineære tilnærmingsmetoden, som fungerer etter prinsippet om å fylle segmentene som nærmer seg med pulser med forskjellige repetisjonshastigheter. Fyllingsfrekvensene endres i hopp ved grensepunktene til segmentene som nærmer seg i henhold til programmet som er satt inn i enheten i henhold til typen ikke-linearitet. Den lineariserte mengden konverteres deretter til en enhetskode.

En delvis lineær tilnærming av ikke-lineariteten kan også utføres ved bruk av en digital lineær interpolator. I dette tilfellet forblir fyllingsfrekvensene til interpolasjonsintervallene konstante bare i gjennomsnitt.

Fordelene med digitale linearisatorer basert på metoden for lineær tilnærming av deler er: enkel rekonfigurering av den akkumulerte ikke-lineariteten og hastigheten på å bytte fra en ikke-linearitet til en annen, noe som er spesielt viktig i høyhastighets sentraliserte kontrollsystemer.

I komplekse kontrollsystemer som inneholder universelle kalkulatorer, maskiner, kan linearisering utføres direkte fra disse maskinene, der funksjonen er innebygd i form av en tilsvarende subrutine.