Prinsippet og metodene for indirekte bestemmelse av effektfaktoren i vekselstrømkretsen

Effektfaktor eller cosinus phi, med hensyn til brukeren av sinusformet vekselstrøm, er forholdet mellom det aktive strømforbruket P og den totale effekten S som tilføres denne brukeren fra nettverket.

Total kraft S, i det generelle tilfellet, kan defineres som produktet av de effektive (root mean square) verdiene av strømmen I og spenningen U i den betraktede kretsen, og den aktive effekten P - som irreversibelt forbrukt av brukeren for drift av arbeidet.

Reaktiv effekt Q, selv om det er en del av den totale kraften, forbrukes det imidlertid ikke for å utføre arbeid, men deltar bare i opprettelsen av vekslende elektriske og magnetiske felt i noen elementer i brukerens krets.

unntatt direkte effektfaktormåling bruk av elektrodynamiske enheter - fasemålere, det er ganske logiske indirekte metoder som lar deg matematisk nøyaktig forstå verdien av denne svært viktige elektriske størrelsen som karakteriserer brukeren i en sinusformet vekselstrømkrets.

La oss se på dataene indirekte metoder i detaljer, La oss forstå prinsippet om indirekte effektfaktormåling.

Voltmeter, amperemeter og wattmeter metode

Elektrodynamisk wattmåler med ekstra aktiv motstand i kretsen til den bevegelige spolen indikerer verdien av ekstremt aktiv strøm forbrukt i AC-kretsen P.

Hvis vi nå, ved hjelp av et voltmeter og et amperemeter, måler gjennomsnittsverdiene av strømmen I og spenningen U som virker i kretsen til lasten som studeres, vil vi ved å multiplisere disse to parameterne bare få den totale effekten S .

Da kan effektfaktoren (cosinus phi) for en gitt last lett finnes ved å bruke formelen:

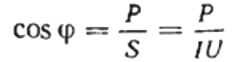
Her, hvis du ønsker det, kan du også finne verdien av den reaktive effekten Q, den totale motstanden til kretsen z Ohms lov, så vel som aktiv og reaktiv motstand, ganske enkelt ved å konstruere eller representere en motstandstrekant, og deretter bruke Pythagoras teorem:

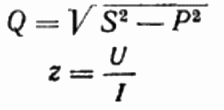
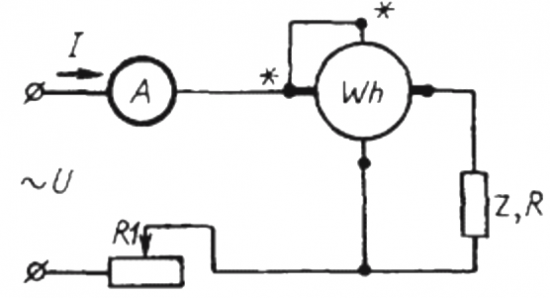
Teller- og amperemetermetode

For å bruke denne metoden er det nødvendig å sette sammen en krets der den enkleste er koblet i serie med belastningen Z og amperemeteret strømmåler Wh.

I en viss tidsperiode t, i størrelsesorden et minutt, vil det være nødvendig å beregne antall omdreininger på disken N, som vil vise mengden aktiv energi brukt i løpet av en gitt tid (dvs. tatt i betraktning maktfaktor).

Her: antall omdreininger til skiven N, koeffisienten k er mengden energi per omdreining, I og U er henholdsvis rms-strømmen og spenningen, t er tiden for å telle omdreiningene, cosinus phi er effektfaktoren:

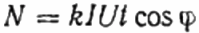
Deretter, i stedet for den studerte brukeren Z, inkluderes den aktive belastningen R i kretsen gjennom den samme telleren, men ikke direkte, men gjennom reostaten R1 (oppnår samme strøm I som i det første tilfellet, med brukeren Z). Antall omdreininger til skiven N1 opprettholdes i samme tid t. Men her, siden lasten er aktiv, er cosinus phi (kraftfaktor) absolutt lik 1. Derfor:

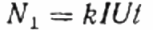
Deretter registreres forholdet mellom omdreininger til disktelleren for samme tidsperiode i det første og andre tilfellet. Dette vil være cosinus phi, det vil si effektfaktoren til den første lasten (i forhold til en rent aktiv last med samme nåværende):

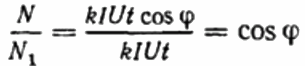
Tre amperemeter metode

For å bestemme effektfaktoren i en sinusformet strømkrets med tre amperemeter, må du først sette sammen følgende krets:

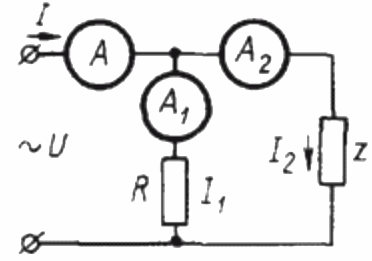
Her er Z en last hvis effektfaktor skal bestemmes og R er en ren aktiv last.

Siden lasten R er rent aktiv, er strømmen I1 til enhver tid i fase med vekselspenningen U påført denne lasten. I dette tilfellet er strømmen I lik den geometriske summen av strømmene I1 og I2. Nå skal vi basert på denne posisjonen bygge et vektordiagram av strømmene:

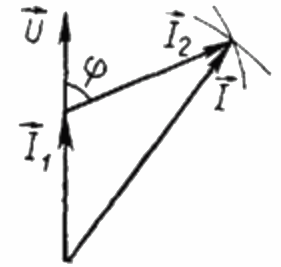
På vektordiagrammet for strømmene er den spisse vinkelen mellom strømmen I1 og strømmen I2 vinkelen phi, hvis cosinus (faktisk verdien av kraftfaktoren) kan finnes fra en spesiell verditabell av trigonometriske funksjoner eller beregnet med formelen:

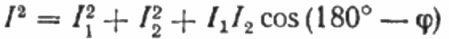
Herfra kan vi uttrykke cosinus phi, det vil si ønsket effektfaktor:

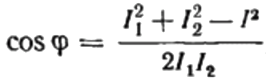
Tegnet på effektfaktoren funnet («+» eller «-«) vil indikere belastningens art. Hvis effektfaktoren (cosinus phi) er negativ, er belastningen kapasitiv. Hvis effektfaktoren er en positiv verdi, er belastningens natur induktiv.