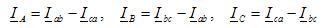Beregning av trefasekretser

Kjede trefaset vekselstrøm består av en trefaset strømforsyning, en trefaset forbruker og kommunikasjonsledningene mellom dem.

En symmetrisk trefase forsyning kan representeres som tre enfase forsyninger som opererer på samme frekvens med samme spenning og med en fasevinkel i tid på 120 °. Disse kildene kan være stjerne- eller deltakoblede.

Når den er koblet i en stjerne, brukes den betingede begynnelsen av fasene til å koble sammen tre lineære ledere A, B, C, og endene av fasene er forent i ett punkt, kalt nøytralpunktet til strømkilden (trefasegenerator eller transformator). Til dette punktet kan kobles en nøytral ledning N. Stjernekoblingsskjemaet til strømkilden er vist i figur 1, a.

Ris. 1. Tilkoblingsskjemaer for strømforsyningsfasene: a — stjerne; b - trekant

Spenningen mellom linje og nullleder kalles fase og mellom linjeledere kalles linje (for mer detaljer se her – Lednings- og fasespenning).

V integrert form oppføringene av uttrykkene for fasespenningene er:

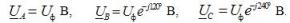
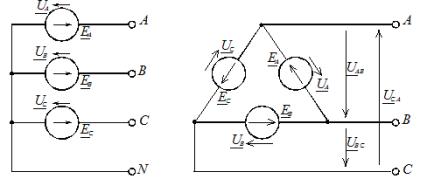
Tilsvarende linjespenninger når stjernekoblet:

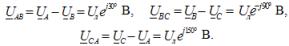
Her er Uf fasespenningsmodulen til strømkilden og Ul er linjespenningsmodulen. I et symmetrisk trefasesystem, når kildefasene er stjernekoblet, er det et forhold mellom disse spenningene:

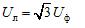
Når fasene er koblet med en trekant, kobles fasestrømforsyningene i serie i en lukket sløyfe (Figur 1, b).

Tre lineære ledninger A, B, C bringes ut fra punktene for å kombinere kildene med hverandre, og går til lasten. Fra figur 1, b, kan det sees at utgangene til fasekildene er koblet til lineære ledninger, og derfor, når fasene til kilden er forbundet med en trekant, er fasespenningene lik lineære. I dette tilfellet er det ingen nøytral ledning.

En last kan kobles til en trefaseforsyning. Når det gjelder størrelse og natur, kan en trefaselast være symmetrisk og asymmetrisk.

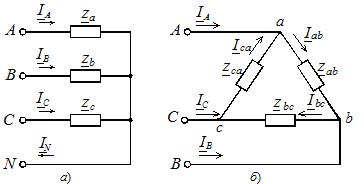
Ved en symmetrisk belastning er de komplekse motstandene til de tre fasene de samme, og hvis disse motstandene er forskjellige, er belastningen ubalansert. Lastfasene kan kobles til hverandre med stjerne eller trekant (Figur 2), uavhengig av kildekoblingsskjemaet.

Ris. 2. Last fasekoblingsskjemaer

Stjernetilkoblingen kan være med eller uten nøytral ledning (se figur 2, a). Fraværet av en nøytral ledning eliminerer den stive tilkoblingen av lastspenningen til forsyningsspenningen, og i tilfelle en asymmetrisk fasebelastning er disse spenningene ikke like med hverandre.For å skille dem ble vi enige om å bruke store bokstaver i bokstavbetegnelsesindeksene for forsyningsspenningene og strømmene, og små bokstaver i de lastspesifikke parameterne.

Algoritmen for å analysere en trefasekrets avhenger av belastningstilkoblingsskjemaet, de første parametrene og formålet med beregningen.

To-node-metoden brukes til å bestemme fasespenningene med en ubalansert stjernekoblet last uten nøytral leder. I henhold til denne metoden begynner beregningen med bestemmelsen av spenningen UN mellom nøytralpunktene til forsyningen og lasten, kalt nøytralavviksspenningen:

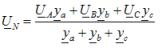
hvor ya, yb, yc - tillatte verdier for de tilsvarende belastningsfasene i kompleks form

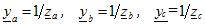
Spenningene over fasene til en ubalansert last er funnet fra uttrykkene:

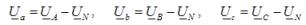
I det spesielle tilfellet med lastubalanse, når det i fravær av en nøytral leder oppstår en kortslutning i en av belastningsfasene, er den nøytrale forspenningen lik fasespenningen til forsyningen til fasen der kortslutningen skjedde.

Spenningen på den lukkede fasen av lasten er null, og på de to andre er den numerisk lik linjespenningen. Anta for eksempel at det oppstår en kortslutning i fase B. Den nøytrale forspenningen for dette tilfellet er UN = UB. Da er fasespenningene på lasten:

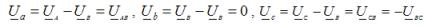
Fasestrømmer i lasten, de er også linjelederstrømmer for alle typer last:

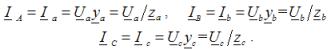
I oppgavene ved beregning av trefasekretser vurderes tre alternativer for å koble trefaseforbrukere med en stjerne: tilkobling til en nøytral ledning i nærvær av forbrukere i tre faser, tilkobling til en nøytral ledning i fravær av forbrukere i en av fasene, og tilkobling uten nøytral ledning med kort forbindelse i en av belastningsfasene...

I den første og andre versjonen er de tilsvarende fasespenningene til forsyningen plassert på belastningsfasene, og fasestrømmene i belastningen bestemmes av formlene ovenfor.

I den tredje versjonen er spenningen til lastfasene ikke lik fasespenningen til forsyningen og bestemmes ved hjelp av avhengighetene

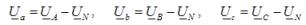
Strømmene i to ukortlagte faser bestemmes i henhold til Ohms lov, som en brøkdel av delingen av fasespenningen med impedansen til den respektive fasen. Kortslutningsstrømmen bestemmes ved hjelp av en ligning basert på Kirchhoffs første lovkompilert for nøytralpunktet til lasten.

For eksempelet ovenfor på en fase B-kortslutning:

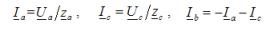
For hver type last er den trefasede aktive og reaktive effekten lik summen av henholdsvis den aktive og reaktive effekten til de enkelte fasene. For å bestemme disse fasekreftene kan du bruke uttrykket

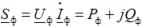
hvor Uf,Azf, er komplekset av spenningen og komplekset av koblede strømmer i belastningsfasen; Pf, Qf — aktiv og reaktiv effekt i belastningsfasen.

Trefase aktiv effekt: P = Pa + Pb + Pc

Trefase reaktiv effekt: Q = Qa + Qb + Vc

Trefaset tilsynelatende kraft:

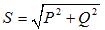
Når forbrukere er forbundet med en trekant, har kretsen formen vist i figur 2, b. I denne modusen er fasetilkoblingen til den balanserte strømforsyningen irrelevant.

Spenninger mellom strømforsyningsledningene detekteres på belastningsfasene. Fasestrømmene i lasten bestemmes vha Ohms lov for en del av en kretsAzf = Uf /zf, hvor Uf — fasespenning i lasten (tilsvarer nettspenningen til strømkilden); zf er den totale motstanden til den tilsvarende fasen av lasten.

Strømmer i lineære ledere bestemmes av fasestrømmer basert på Kirchhoffs første lov for hver node (punktene a, b, c) i kretsen vist i figur 2, b: