Potensielt kretsskjema

Et diagram av potensialet kalles en grafisk representasjon av fordelingen av det elektriske potensialet langs en lukket sløyfe, avhengig av motstanden til seksjonene som er inkludert i den valgte sløyfen.

En lukket sløyfe er valgt for å konstruere et potensialdiagram. Denne kretsen er delt inn i seksjoner på en slik måte at det er én bruker eller energikilde per seksjon. Grensepunkter mellom seksjoner skal merkes med bokstaver eller tall.

Ett punkt i sløyfen er vilkårlig jordet, potensialet anses betinget som null. Går du rundt konturen med klokken fra et punkt med nullpotensial, er potensialet til hvert påfølgende grensepunkt definert som den algebraiske summen av potensialet til det forrige punktet og endringen av potensialet mellom disse tilstøtende punktene.

Endringen i potensialet til et objekt avhenger av sammensetningen av kretsen mellom punktene. Hvis en strømforbruker (motstand) er inkludert i plasseringen, er endringen i potensial numerisk lik spenningsfallet over den motstanden. Tegnet på denne endringen bestemmes av strømmens retning.Hvis strøm- og bypass-retningene til sløyfen stemmer overens, er tegnet negativt, ellers er det positivt.

Hvis det er en EMF-kilde på objektet, er den potensielle endringen her numerisk lik EMF-verdien til denne kilden. Hvis omløpsretningen til sløyfen og retningen til EMF faller sammen, er den potensielle endringen positiv, ellers er den negativ.

Etter å ha beregnet potensialene til alle punktene, konstrueres et potensialdiagram i et rektangulært koordinatsystem. På abscisseaksen er motstanden til seksjonene tegnet i skala i rekkefølgen de møtes i når de krysser konturen, og på ordinaten, potensialene til de tilsvarende punktene. Potensialdiagrammet starter ved null potensial og slutter etter å ha syklet gjennom det.

Konstruer et potensialkretsskjema

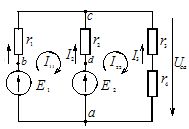
I dette eksemplet konstruerer vi et potensialdiagram for den første sløyfen i kretsen hvis diagram er vist i figur 1.

Ris. 1. Diagram over en kompleks elektrisk krets

Den betraktede kretsen inkluderer to strømforsyninger E1 og E2, samt to strømforbrukere r1, r2.

Vi deler denne konturen i seksjoner, hvis grenser er indikert med bokstavene a, b, c, d. Vi jorder punkt a, konvensjonelt vurderer dets potensial til å være null, og sirkler konturen med klokken fra dette punktet. Derfor er φα = 0.

Det neste punktet på stien for å krysse konturen vil være punkt b. EMF-kilden E1 er plassert i seksjon ab. Når vi beveger oss fra den negative til den positive polen til kilden i denne delen, øker potensialet med verdien E1:

φb = φa + E1 = 0 + 24 = 24 V

Når du beveger deg fra punkt b til punkt c, avtar potensialet med størrelsen på spenningsfallet over motstanden r1 (bypassretningen til sløyfen faller sammen med retningen til strømmen i motstanden r1):

φc = φb — Az1r1 = 24 — 3 x 4 = 12V

Når du går til punkt d, øker potensialet med mengden spenningsfall over motstand r2 (i denne delen er strømretningen motsatt av retningen til sløyfeomløpet):

φd = φ° C + I2r2 = 12 + 0 NS 4 = 12 V

Potensialet til punkt a er mindre enn potensialet til punkt d med verdien av EMF til kilden E2 (retningen til EMF er motsatt av retningen for å omgå kretsen):

φa = φd — E2 = 12 — 12 = 0

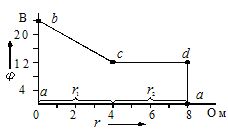
Resultatene av beregningene brukes til å bygge et potensialdiagram. På abscisseaksen er motstanden til seksjonene plottet i serie, slik den ville vært når kretsen er omgitt av et nullpotensial. De tidligere beregnede potensialene til de tilsvarende punktene er plottet langs ordinaten (fig. 2).

Tegning 2... Potensialkonturdiagram

Patskevich V.A.