Tidskonstanten til en elektrisk krets - hva den er og hvor den brukes

Periodiske prosesser er iboende i naturen: dag etterfølges av natt, den varme årstiden erstattes av kulden, etc. Perioden for disse hendelsene er nesten konstant og kan derfor bestemmes strengt. Dessuten har vi rett til å hevde at de periodiske naturlige prosessene som er nevnt som eksempel, ikke avskriver, i det minste når det gjelder en persons levetid.

Men i teknologi, innen elektroteknikk og elektronikk, spesielt, er ikke alle prosesser periodiske og kontinuerlige. Vanligvis øker noen elektromagnetiske prosesser først og avtar deretter. Ofte er materie bare begrenset til fasen av begynnelsen av oscillasjonen, som ikke har tid til å virkelig ta fart.

Ganske ofte kan man i elektroteknikk finne såkalte eksponentielle transienter, hvis essens er at systemet rett og slett streber etter å nå en eller annen likevektstilstand, som til slutt ser ut som en hviletilstand. En slik overgang kan enten være økende eller avtagende.

Den ytre kraften bringer først det dynamiske systemet ut av likevekt, og forhindrer deretter ikke den naturlige tilbakeføringen av dette systemet til sin opprinnelige tilstand. Denne siste fasen er den såkalte overgangsprosessen, som er preget av en viss varighet. I tillegg er prosessen med å ubalansere systemet også en forbigående prosess med en karakteristisk varighet.

På en eller annen måte, tidskonstanten til den forbigående prosessen, kaller vi dens tidskarakteristikk, som bestemmer tiden etter hvilken en viss parameter i denne prosessen vil endre tidene «e», det vil si at den vil øke eller redusere med omtrent 2,718 ganger sammenlignet med utgangstilstanden.

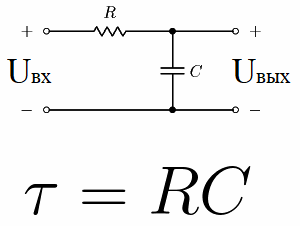
Tenk for eksempel på en elektrisk krets som består av en likespenningskilde, en kondensator og en motstand. Denne typen kretser hvor en motstand er koblet i serie med en kondensator kalles en RC-integreringskrets.

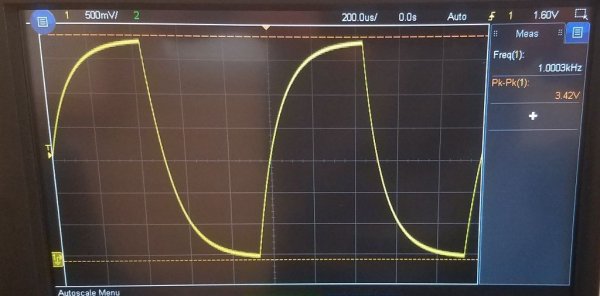
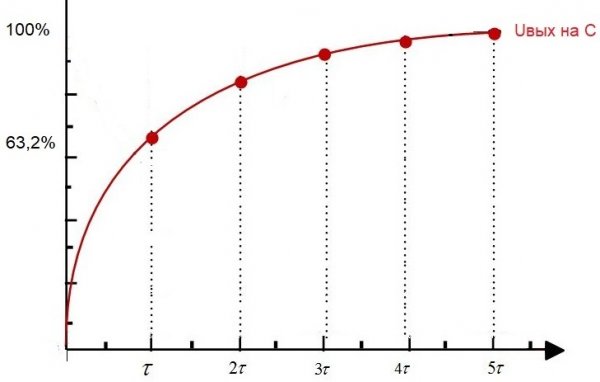
Hvis i det første øyeblikket for å levere strøm til en slik krets, det vil si å sette en konstant spenning Uin ved inngangen, vil Uout — spenningen i kondensatoren begynne å vokse eksponentielt.

Etter tid t1 vil kondensatorspenningen nå 63,2 % av inngangsspenningen. Så, tidsintervallet fra det første øyeblikket til t1 er tidskonstanten til denne RC-kretsen.

Denne kjedekonstanten kalles «tau», målt i sekunder og indikert med dens tilsvarende greske bokstav. Numerisk, for en RC-krets, er den lik R * C, der R er i ohm og C er i farad.

Integrerende RC-kretser brukes i elektronikk som lavpassfiltre når høyere frekvenser må kuttes (undertrykkes) og lavere frekvenser må føres gjennom.

I praksis er mekanismen for slik filtrering basert på følgende prinsipp. For vekselstrøm fungerer kondensatoren som en kapasitiv motstand, hvis verdi er omvendt proporsjonal med frekvensen, det vil si at jo høyere frekvensen er, jo lavere vil reaktansen til kondensatoren i ohm være.

Derfor, hvis en vekselstrøm føres gjennom RC-kretsen, vil, som på armen til spenningsdeleren, en viss spenning falle over kondensatoren, proporsjonal med dens kapasitans ved frekvensen til strømmen som passeres.

Hvis avskjæringsfrekvensen og amplituden til inngangsvekselsignalet er kjent, vil det ikke være vanskelig for designeren å velge en slik kondensator og motstand i RC-kretsen, slik at minimum (avskjærings)spenning (for cut-off frekvens — den øvre grensen for frekvensen) faller på kondensatoren, siden reaktansen går inn i deleren sammen med en motstand.

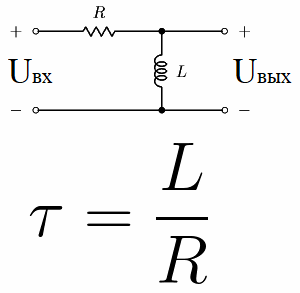
Vurder nå den såkalte differensieringskretsen. Det er en krets som består av en motstand og en induktor koblet i serie, en RL-krets. Tidskonstanten er numerisk lik L / R, der L er induktansen til spolen i henries og R er motstanden til motstanden i ohm.

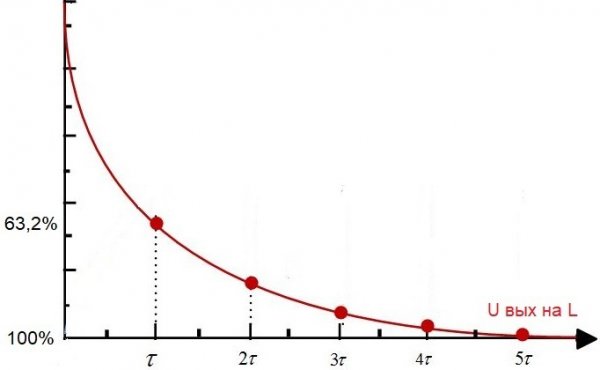
Hvis en konstant spenning fra en kilde påføres en slik krets, vil spenningen til spolen etter en tid reduseres med 63,2 % sammenlignet med U in, det vil si i full overensstemmelse med verdien av tidskonstanten for denne elektriske kretsen .

I AC-kretser (vekslende signaler) brukes LR-kretser som høypassfiltre når lave frekvenser må kuttes (undertrykkes) og frekvenser over (over grensefrekvensen - den nedre frekvensgrensen) - er utelatt.Så jo høyere induktans av spolen, jo høyere frekvens.

Som i tilfellet med RC-kretsen diskutert ovenfor, brukes spenningsdelerprinsippet her. En høyere frekvens strøm som går gjennom RL-kretsen vil resultere i et større spenningsfall over induktansen L, som med den induktive motstanden som er en del av spenningsdeleren sammen med motstanden. Konstruktørens oppgave er å velge slike R og L slik at minimum (grense)spenning til spolen oppnås nøyaktig ved grensefrekvensen.