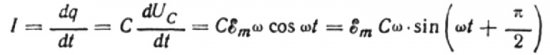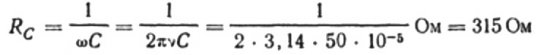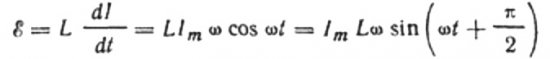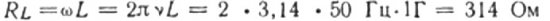Kapasitiv og induktiv motstand i en vekselstrømkrets

Hvis vi inkluderer en kondensator i en DC-krets, finner vi at den har uendelig motstand fordi en likestrøm rett og slett ikke kan passere gjennom dielektrikumet mellom platene, siden et dielektrikum per definisjon ikke leder en elektrisk likestrøm.

En kondensator bryter likestrømskretsen. Men hvis den samme kondensatoren nå er inkludert i vekselstrømkretsen, viser det seg at kondensatoren ikke ser ut til å gå helt i stykker, den veksler og lades, det vil si at den elektriske ladningen beveger seg, og strømmen i den eksterne kretsen er opprettholdt.

Basert på Maxwells teori i dette tilfellet kan vi si at vekselledningsstrømmen inne i kondensatoren fortsatt er lukket, bare i dette tilfellet - av forspenningsstrømmen. Dette betyr at kondensatoren i AC-kretsen fungerer som en type motstand med endelig verdi. Denne motstanden kalles kapasitiv.

Praksis har lenge vist at mengden vekselstrøm som flyter gjennom en leder avhenger av formen til den lederen og av de magnetiske egenskapene til mediet rundt den.Med en rett ledning vil strømmen være størst, og hvis den samme ledningen vikles inn i en spole med et stort antall omdreininger, blir strømmen mindre.

Og hvis en ferromagnetisk kjerne introduseres i samme spole, vil strømmen avta enda mer. Derfor gir ledningen vekselstrøm ikke bare med en ohmsk (aktiv) motstand, men også med en ekstra motstand, avhengig av ledningens induktans.Denne motstanden kalles induktiv.

Dens fysiske betydning er at en skiftende strøm i en leder med en viss induktans initierer en EMF av selvinduksjon i den lederen, som har en tendens til å forhindre endringer i strømmen, det vil si har en tendens til å redusere strømmen. Dette tilsvarer å øke motstanden til ledningen.

Kapasitans i AC-kretsen

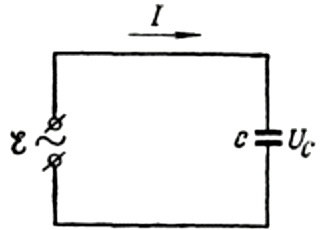
Først, la oss snakke om kapasitiv motstand mer detaljert. Anta at en kondensator med kapasitans C er koblet til en sinusformet vekselstrømkilde, så vil EMF til denne kilden bli beskrevet med følgende formel:

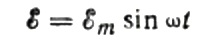
Vi vil ignorere spenningsfallet over tilkoblingsledningene, da det vanligvis er veldig lite og kan vurderes separat om nødvendig. La oss nå anta at spenningen over kondensatorplatene er lik AC-kildespenningen. Deretter:

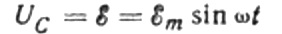
Til enhver tid avhenger ladningen på en kondensator av kapasitansen og spenningen mellom platene. Så, gitt den kjente kilden som ble nevnt ovenfor, får vi et uttrykk for å finne ladningen på kondensatorplatene ved kildespenningen:

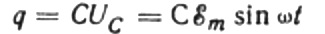
La i en uendelig liten tid dt ladningen på kondensatoren endres med dq, så vil en strøm I flyte gjennom ledningene fra kilden til kondensatoren lik:

Verdien av gjeldende amplitude vil være lik:

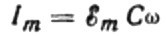
Da vil det endelige uttrykket for strømmen være:

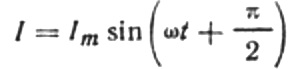
La oss omskrive gjeldende amplitudeformel som følger:

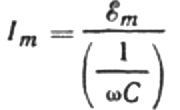
Dette forholdet er Ohms lov, der den resiproke av produktet av vinkelfrekvens og kapasitans spiller rollen som motstand, og er faktisk et uttrykk for å finne kapasitansen til en kondensator i en sinusformet vekselstrømkrets:

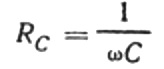
Dette betyr at den kapasitive motstanden er omvendt proporsjonal med vinkelfrekvensen til strømmen og kapasitansen til kondensatoren. Det er lett å forstå den fysiske betydningen av denne avhengigheten.

Jo større kapasitansen til kondensatoren i AC-kretsen og jo oftere retningen til strømmen i den kretsen endres, til slutt passerer mer total ladning per tidsenhet gjennom tverrsnittet av ledningene som kobler kondensatoren til AC-kilden. Dette betyr at strømmen er proporsjonal med produktet av kapasitansen og vinkelfrekvensen.

La oss for eksempel beregne kapasitansen til en kondensator med en elektrisk kapasitet på 10 mikrofarad for en sinusformet vekselstrømkrets med en frekvens på 50 Hz:

Hvis frekvensen var 5000 Hz, ville den samme kondensatoren gi en motstand på omtrent 3 ohm.

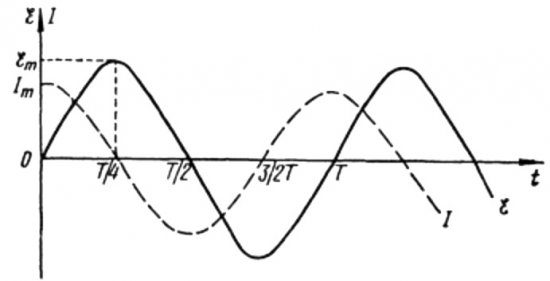
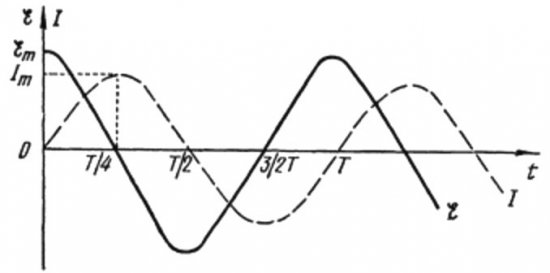
Fra formlene ovenfor er det klart at strømmen og spenningen i en AC-krets med en kondensator alltid endres i forskjellige faser. Strømfasen leder spenningsfasen med pi / 2 (90 grader). Dette betyr at maksimal strøm i tid alltid eksisterer en kvart periode tidligere enn maksimal spenning. På tvers av den kapasitive motstanden leder strømmen altså spenningen med en fjerdedel av tidsperioden, eller med 90 grader i fase.

La oss forklare den fysiske betydningen av dette fenomenet.Ved første øyeblikk er kondensatoren fullstendig utladet, så den minste spenningen som påføres den flytter allerede ladningene på kondensatorplatene, og skaper en strøm.

Når kondensatoren lades, øker spenningen over platene, dette forhindrer ytterligere strøm av ladning, slik at strømmen i kretsen avtar til tross for ytterligere økninger i spenningen som påføres platene.

Dette betyr at hvis strømmen i det første øyeblikket var maksimal, vil strømmen stoppe helt når spenningen når sitt maksimum etter en kvart periode.

I begynnelsen av perioden er strømmen maksimal og spenningen er minimum og begynner å øke, men etter en fjerdedel av perioden når spenningen et maksimum, men strømmen har allerede sunket til null på dette tidspunktet. Dermed viser det seg at spenningen leder spenningen med en fjerdedel av perioden.

AC induktiv motstand

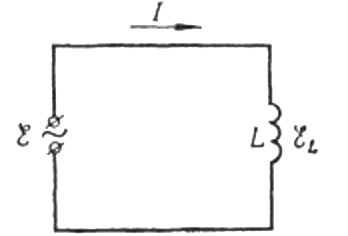
Nå tilbake til induktiv motstand. Anta at en sinusformet vekselstrøm flyter gjennom en induktansspole. Det kan uttrykkes som:

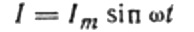
Strømmen skyldes vekselspenningen på spolen. Dette betyr at en EMF av selvinduksjon vil vises på spolen, som uttrykkes som følger:

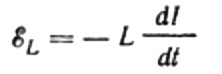
Igjen neglisjerer vi spenningsfallet over ledningene som kobler EMF-kilden til spolen. Deres ohmske motstand er svært lav.

La vekselspenningen påført spolen til enhver tid være fullstendig balansert av den oppståtte EMF av selvinduksjon som er lik den i størrelse, men motsatt i retning:

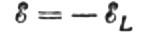
Da har vi rett til å skrive:

Siden amplituden til spenningen påført spolen er:

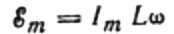
vi får:

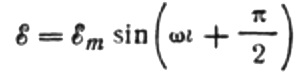
La oss uttrykke den maksimale strømmen som følger:

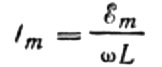
Dette uttrykket er i hovedsak Ohms lov. En mengde lik produktet av induktansen og vinkelfrekvensen spiller rollen som motstand her og er ikke annet enn induktorens induktive motstand:

Så den induktive motstanden er proporsjonal med induktansen til spolen og vinkelfrekvensen til vekselstrømmen gjennom den spolen.

Dette skyldes det faktum at induktiv motstand skyldes påvirkning av selvinduksjons-EMF på kildespenningen, - selvinduksjons-EMK har en tendens til å redusere strømmen og bringer derfor motstand i kretsen. Størrelsen på selvinduksjonens emk er som kjent proporsjonal med spolens induktans og endringshastigheten til strømmen gjennom den.

La oss for eksempel beregne den induktive motstanden til en spole med en induktans på 1 H, som er inkludert i en krets med en strømfrekvens på 50 Hz:

Hvis frekvensen til kulen var 5000 Hz, ville motstanden til den samme spolen være omtrent 31 400 ohm. Husk at den ohmske motstanden til spoleledningen vanligvis er noen få ohm.

Fra formlene ovenfor er det åpenbart at endringene i strømmen gjennom spolen og spenningen i den skjer i forskjellige faser, og strømmens fase er alltid mindre enn fasen til spenningen ved pi / 2. Derfor maksimal strøm oppstår en kvart periode senere enn inntreden av maksimal stress.

I induktiv motstand forsinker strømmen spenningen med 90 grader på grunn av bremseeffekten til den selvinduserte EMF, som hindrer strømmen i å endre seg (både økende og avtagende), slik at den maksimale strømmen observeres i kretsen med spolen senere enn maksimal spenning.

Spole og kondensator kombinert handling

Hvis du kobler en spole med en kondensator i serie med en vekselstrømkrets, så vil spolespenningen øke kondensatorspenningen i tid med en halv periode, det vil si med 180 grader i fase.

Kapasitiv og induktiv motstand kalles reaktanter… Energi brukes ikke på reaktiv motstand som i aktiv motstand. Energien som er lagret i kondensatoren returneres periodisk tilbake til kilden når det elektriske feltet i kondensatoren forsvinner.

Det er det samme med en spole: Ettersom spolens magnetfelt skapes av strømmen, akkumuleres energien i den i løpet av en fjerdedel av perioden, og i løpet av neste fjerdedel av perioden går den tilbake til kilden. I denne artikkelen har vi snakket om sinusformet vekselstrøm, som disse forskriftene følges strengt.

I sinusformede AC-kretser kalles kjerneinduktorer kvelesbrukes tradisjonelt for strømbegrensning. Deres fordel i forhold til reostater er at energi ikke spres i store mengder som varme.