Kretstopologier—Grunnleggende konsepter

En elektrisk krets er et sett med enheter (elementer) og deres forbindelsesledninger som en elektrisk strøm kan flyte gjennom. Alle elementer i elektriske kretser deler i passiv og aktiv.

Aktive elementer omdanner ulike typer energi (mekanisk, kjemisk, lys, etc.) til elektrisk energi. I passive enheter omdannes elektrisk energi til andre typer energi. Aktive elementer kalles kilder, passive kalles forbrukere eller mottakere.

I kretsteori vurderes idealiserte modeller av elektriske elementer. Dette gjør beskrivelsen av elementene så enkel som mulig. Mer komplekse, virkelige elementer er modellert fra et sett med idealiserte elementer.

De viktigste passive elementene i elektriske kretser er motstand (resistivt element), induktor (induktivt element) og kondensator (kapasitivt element). Elementer er installert i en elektrisk krets for å generere spenning og strøm av en gitt verdi og form (se - Elektrisk krets og dens elementer).

En elektrisk krets består av grener og noder. gren — dette er en del av en elektrisk krets (krets) som den samme strømmen flyter gjennom. En knute — tilkobling av tre eller flere grener. På det elektriske diagrammet er noden indikert med en prikk (fig. 1).

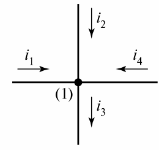
Ris. 1. Definer noden i diagrammet

Om nødvendig er nodene i diagrammet nummerert fra venstre til høyre fra topp til bunn.

I fig. 2 viser den resistiv-kapasitive grenen i hvilken strømmen iC flyter.

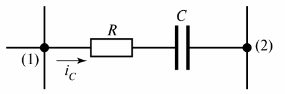
Ris. 2. Resistiv-kapasitiv gren

En annen definisjon av en gren kan gis - det er en del av en krets mellom to tilstøtende noder (noder (1) og (2) i fig. 2).

Kjede Er det noen lukket bane i den elektriske kretsen. Kretsen kan lukkes av alle grener, inkludert betingede grener hvis motstand er lik uendelig.

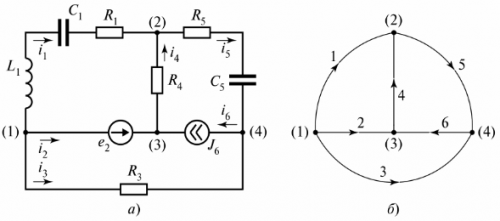
I fig. 3 viser en forgrenet elektrisk krets som består av tre grener.

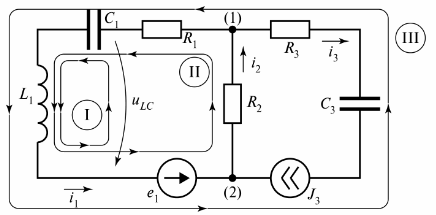
Ris. 3. Elektrisk krets med to kretser

Diagrammet viser tre kretser, og krets I er lukket av en gren med uendelig motstand. Denne grenen er indikert som spenning tiLC.

For kretsen på fig. 3 er det mulig å komponere mange sløyfer som er lukket av reelle eller betingede grener, men for beregning av elektrisk støy brukes begrepet «uavhengig sløyfe». Antall uavhengige kretssløyfer er alltid satt som minimum som kreves for beregningen.

Uavhengige kretser er alltid lukket, men grener som har en motstand som ikke er lik uendelig, og hver uavhengig krets inkluderer minst en gren som ikke er inkludert i andre kretser. For komplekse elektriske kretser kan du bestemme antall uavhengige kretser ved hjelp av kretsskjemaet.

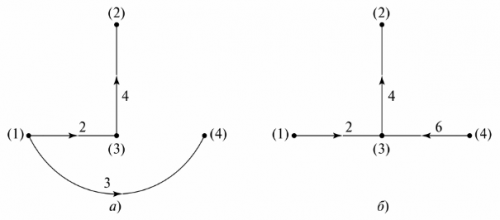
På kretsskjemaet en betinget representasjon av kretsen kalles, der hver gren er erstattet av et linjesegment. Elementer i grener vises ikke. For eksempel, i fig. 4 viser en grenkrets og dens diagram.

Ris. 4. Forgrenet elektrisk krets: a — kretsskjema, b — diagram

For å lage et diagram av et diagram, må du koble nodene med grenlinjer uten å spesifisere elementer på dem. Grenene er nummerert, og retningene til strømmene på dem er indikert med piler. Selve grafen har ingen fysisk betydning, men kan brukes til å bestemme antall og type uavhengige konturer. For dette formålet utarbeides et "grafisk tre".

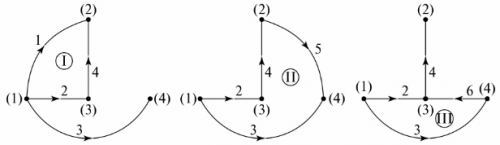
Grafisk tre Den representerer grafen til en krets hvis noder er forbundet med grener på en slik måte at ingen lukket sløyfe resulterer. Det kan være flere alternativer for å vise et grafisk tre. I fig. 5 viser to mulige alternativer for kretsen på fig. 4.

Ris. 5. Grafisk tre av ordningen

Antallet manglende grener i graftreet er lik antallet uavhengige sløyfer i kretsen. I eksemplet er dette tre grener, tre uavhengige løkker. Konfigurasjonen av uavhengige sløyfer kan oppnås ved å sekvensielt koble nodene til graftreet med grener som ikke er spesifisert på graftreet. For eksempel, for graftreet i fig. 5, og de uavhengige konturene er vist i fig. 6.

Ris. 6. Bestemme uavhengige konturer gjennom graftreet

Valget av et alternativ for å konfigurere uavhengige kretser for beregning av kretsen utføres under kretsanalyse. Du bør velge slike konturer slik at beregningen er så enkel som mulig, d.v.s. antall avhengige ligninger i systemet er minimalt.

Topologiske ligninger etablerer en sammenheng mellom spenninger og strømmer i en krets, og antall og type ligninger er ikke avhengig av hvilke elementer som inngår i grenene. Topologiske ligninger inkluderer ligninger sammensatt av i henhold til Kirchhoffs lover.