Trefaset strømforsyning: aktiv, reaktiv, full

Verdiene av den totale aktive og totale reaktive effekten til den trefasede kretsen er lik summen av den aktive og reaktive effekten for hver av de tre fasene A, B og C, henholdsvis. Denne påstanden er illustrert av følgende formler:

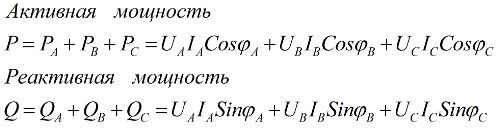
her er Ua, Ub, Uc, Ia, Ib, Ic verdiene av fasespenninger og strømmer og φ er faseforskyvningen.

Når belastningen er symmetrisk, det vil si under forhold der den aktive og reaktive effekten til hver av fasene er lik hverandre, for å finne den totale effekten til flerfasekretsen, er det nok å multiplisere verdien av faseeffekten med antall involverte faser. Den totale effekten bestemmes basert på de oppnådde verdiene av dens aktive og reaktive komponenter:

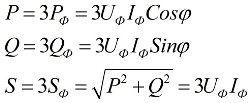
I formlene ovenfor kan faseverdiene til mengdene uttrykkes i form av deres lineære verdier, som vil variere for stjerne- eller deltaforbindelsesskjemaer for brukere, men kraftformlene vil til slutt være de samme:

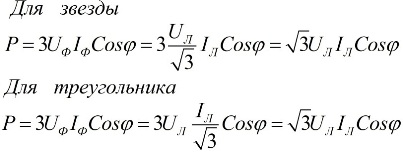
Det følger av uttrykkene ovenfor at uavhengig av tilkoblingsskjemaet til mottakerne av elektrisk energi, enten det er en trekant eller en stjerne, hvis belastningen er symmetrisk, vil formlene for å finne kraften ha samme form, både for en trekant og for en stjerne:

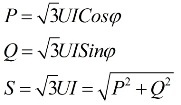
Disse formlene viser lineære verdier for spenning og strøm og er skrevet uten abonnenter. Vanligvis finnes en slik notasjon, uten subscripts, det vil si at hvis det ikke er noen subscripts, mener vi lineære verdier.

En spesiell måleenhet, kalt wattmåler… Målingene bestemmes av formelen:

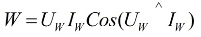
i formelen ovenfor er Uw og Iw vektorene for spenningen som påføres lasten og strømmen som flyter gjennom den.

Arten av den aktive lasten og fasekoblingsdiagrammet kan være forskjellig, derfor vil koblingsdiagrammene til wattmåleren være forskjellige, avhengig av de spesifikke omstendighetene.

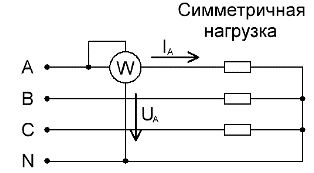
For symmetrisk belastede trefasekretser, for en grov måling av den totale aktive effekten, hvis høy nøyaktighet ikke er nødvendig, er ett wattmeter koblet til bare en av fasene tilstrekkelig. Etter det, for å få verdien av den aktive kraften til hele kretsen, gjenstår det å multiplisere avlesningene til wattmåleren med antall faser:

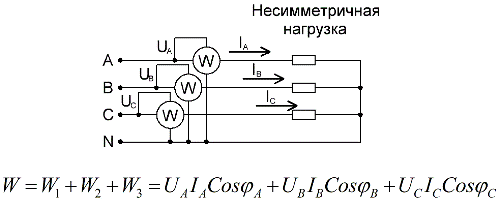
For en fire-leder krets med en nøytral ledning, for nøyaktig å måle aktiv effekt, kreves tre wattmeter, som hver avleses og deretter summeres for å få en verdi for den totale effekten til kretsen:

Hvis det ikke er en nøytral ledning i en trefasekrets, er to wattmeter tilstrekkelig til å måle den totale effekten, selv om belastningen er ubalansert.

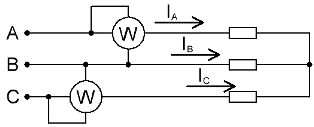
I fravær av en nøytral leder er fasestrømmene sammenkoblet i henhold til Kirchhoffs første lov:

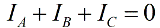
Da vil summen av avlesningene til et par wattmålere være lik:

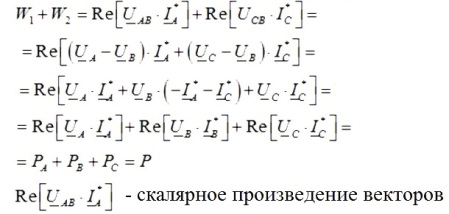
Så hvis du legger til avlesningene til et par wattmålere, får du den totale aktive effekten i trefasekretsen som studeres, og avlesningene til wattmålerne vil avhenge av både størrelsen på lasten og dens natur.

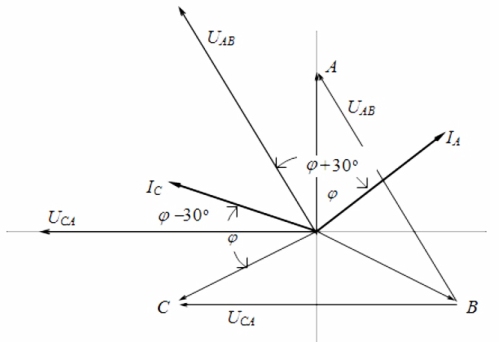
Ser vi på vektordiagrammet for strømmer og spenninger i forbindelse med en symmetrisk belastning, kan det konkluderes med at avlesningene til wattmetre bestemmes av følgende formler:

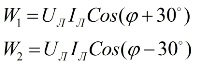
Etter å ha analysert disse uttrykkene, kan det forstås at med en rent aktiv belastning, når φ = 0, vil avlesningene til de to wattmetrene være lik hverandre, det vil si W1 = W2.

Med aktiv lastinduktans, når 0 ≤ φ ≤ 90 °, vil avlesningene til wattmeter 1 være mindre enn de for wattmeter 2, det vil si W1 60 °, vil avlesningene til wattmeter 1 være negative, det vil si W1 <0.

Med en aktiv-kapasitiv karakter av lasten, når 0 ≥ φ≥ -90 °, vil avlesningene til wattmeteret 2 være mindre enn wattmeteret 1, det vil si W1> W2. Ved φ <-60 ° vil avlesningene til wattmåleren 2 bli negative.