Overspenning i transformatorviklingene

Dimensjonering og designvalg av transformatorisolasjon er umulig uten å bestemme spenningene som virker på ulike deler av transformatorisolasjonen under drift og testing designet for å sikre pålitelig drift av transformatoren.

I dette tilfellet er spenningene som virker på transformatorisolasjonen når lynbølger treffer inngangen, ofte avgjørende. Disse spenningene, også kalt impulsspenninger, bestemmer i nesten alle tilfeller valget av langsgående viklingsisolasjon og i mange tilfeller hovedviklingsisolasjon, koblingsanordningsisolasjon, etc.

Bruken av datateknologi for å bestemme overspenninger gjør det mulig å gå fra en kvalitativ vurdering av impulsprosesser i viklinger til direkte beregninger av overspenninger og introduksjonen av resultatene deres i designpraksis.

For å beregne overspenningen er transformatorens viklinger representert av en ekvivalent krets som reproduserer induktive og kapasitive forbindelser mellom elementene i viklingen (Figur 1).Alle ekvivalente kretser vurderer kapasitansen mellom svinger og mellom viklinger.

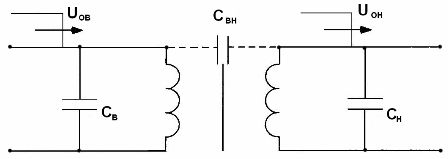
Figur 1. Ekvivalent krets for transformatoren: UOV — innfallende bølge i høyspenningsviklingen, UOH — innfallsbølge i lavspentviklingen, SV og CH — kapasitanser mellom svingene til henholdsvis høyspentviklingen, SVN — kapasitans mellom viklinger med høy og lav spenning.

Bølgeprosesser i transformatorer

Transformatoren vil betraktes som et induktivt element, tatt i betraktning interturn-kapasitansen, kapasitansene mellom skjermen og induktansen, og mellom induktansen og jord (Figur 2a).

Følgende formler brukes til å beregne overspenning:

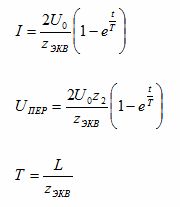
hvor: t er tiden etter ankomsten av bølgen til transformatoren, T er overspenningstidskonstanten, ZEKV er den ekvivalente kretsmotstanden, Z2 er linjemotstanden, Uo er overspenningen ved starttidspunktet

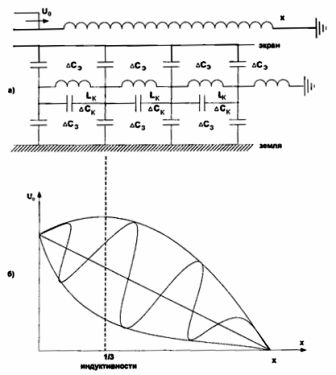
Figur 2. Utbredelse av en spenningsbølge langs viklingen til en transformator med en jordet nøytral: a) skjematisk diagram, b) avhengighet av spenningsbølgen av lengden av viklingen for en enfaset transformator med en jordet terminal: Uo — fallspenningsbølge, ∆Ce — kapasitans mellom spolen og skjermen, ∆Ck — iboende kapasitans mellom svingene, ∆С3 — kapasitans mellom spolen og bakken, ∆Lк — induktans til spolelagene.

Siden det er både induktans og kapasitans i den ekvivalente kretsen, oppstår det en oscillerende LC-krets (spenningsfluktuasjonene er vist i figur 2b).

Amplituden til oscillasjonene er 1,3 — 1,4 av amplituden til den innfallende bølgen, dvs.Uпep = (1,3-1,4) Uo, og den største verdien av overspenning vil oppstå ved slutten av den første tredjedelen av viklingen, derfor, i konstruksjonen av transformatoren, har 1/3 av viklingen forsterket isolasjon sammenlignet med resten .

For å unngå overspenning må ladestrømmen til kondensatorene i forhold til jord kompenseres. For dette formålet er en ekstra skjerm (skjold) installert i kretsen. Ved bruk av skjermen vil kapasitansene til viklingene til skjermen være lik kapasitansen til svingene til jord, dvs. ∆CE = ∆C3.

Skjerming utføres i transformatorer med spenningsklasse UH = 110 kV og høyere. Skjermen er vanligvis installert i nærheten av transformatorhuset.

Enfase transformatorer med isolert nøytral

Tilstedeværelsen av en isolert nøytral betyr at det er en kapasitans Co mellom jord og vikling, dvs. at kapasitansen legges til den ekvivalente kretsen til jordklemmetransformatoren, men skjermen fjernes (Figur 3a).

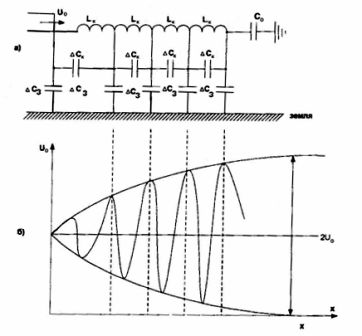
Figur 3. Utbredelse av en spenningsbølge langs viklingen til en transformator med en isolert nøytral: a) skjematisk diagram av en ekvivalent transformator, b) avhengigheten av den innfallende bølgespenningen av viklingens lengde.

En oscillerende krets er også dannet med denne ekvivalente kretsen. På grunn av kapasitansen Co er det imidlertid en oscillerende LC-krets med seriekobling av induktans og kapasitans. I dette tilfellet, med en betydelig kapasitans Co, vil den høyeste spenningen vises på slutten av viklingen (overspenningen kan nå verdier opp til 2Uo). Naturen til spenningsendringen over spolen er vist i figur 3b.

For å redusere amplituden til overspenningsoscillasjoner i viklingen av en transformator med en isolert nøytral, er det nødvendig å redusere kapasitansen til utgangen C i forhold til jord eller å øke selvkapasitansen til spolene. Sistnevnte metode brukes vanligvis. For å øke selvkapasitansen ∆Ck mellom spolene til høyspenningsviklingen, er spesielle kondensatorplater (ringer) inkludert i kretsen.

Bølgeprosesser i trefasetransformatorer

I trefasetransformatorer påvirkes arten av den innfallende bølgeforplantningsprosessen langs viklingen og størrelsen på overspenninger av:

a) spolekoblingsskjema,

b) antall faser som bølgebølgen kommer til.

En trefase transformator med en høyspenningsvikling, stjerne koblet til en solid jordet nøytral

La den innfallende overspenningsbølgen komme inn i en fase av transformatoren (Figur 4).

Prosessene for forplantning av overspenningsbølger langs viklingene vil i dette tilfellet være lik prosessene i en enfaset transformator med en jordet nøytral (i hver av fasene vil den høyeste spenningen være i 1/3 av viklingen), mens de er ikke avhengige av hvor mye faser som når bølgebølgen. Disse. verdien av overspenningen i denne delen av spolen er lik Upep = (1,3-1,4) Uo

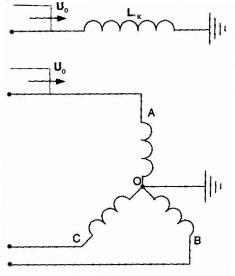
Figur 4. Ekvivalent krets av en trefase transformator med en høyspenningsvikling koblet til en stjerne med et nøytralt jordet nettverk. Overspenningsbølgen kommer i én fase.

Trefaset stjernekoblet høyspenttransformator med isolert nøytral

La bølgebølgen komme i én fase.Den ekvivalente kretsen til transformatoren, samt forplantningen av den innfallende bølgen i transformatorviklingen, er vist i figur 5.

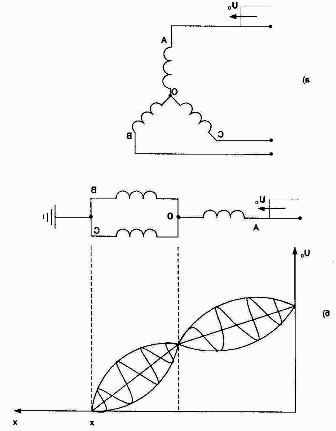
Figur 5. Ekvivalent krets av en trefase transformator med en stjernekoblet høyspenningsvikling (a) og avhengigheten U = f (x) for tilfellet når bølgen kommer i en fase (b).

I dette tilfellet vises to separate oscillasjonssoner. I fase A vil det være ett oscillasjonsområde og forholdene de oppstår under, og i fase B og C vil det være en annen oscillasjonssløyfe, svingeområdet vil også være forskjellig i begge tilfeller. Den største overspenningen vil være på viklingen som mottar den innfallende overspenningsbølgen. Ved nullpunktet er overspenninger opptil 2/3 Uo mulig (i normal modus i dette øyeblikket U = 0, derfor er overspenninger i forhold til driftsspenningen U-drift de farligste for det, siden U0 >> U-drift).

La overspenningsbølgen passere gjennom to faser A og B. Den ekvivalente kretsen til transformatoren samt den innfallende bølgeutbredelsen i transformatorviklingen er vist i figur 6.

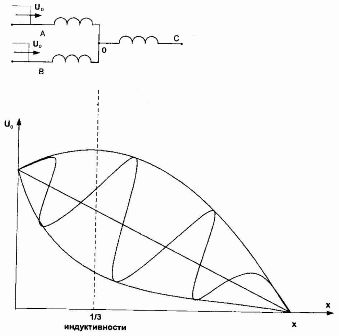
Figur 6. Ekvivalent krets av en trefase transformator med en stjernekoblet høyspenningsvikling (a) og avhengigheten U = f (x) for tilfellet når bølgen kommer i to faser.

I viklingene til fasene som bølgen kommer til, vil spenningen være (1,3 — 1,4) Uo. Nøytralspenningen er 4/3 Uo. For å beskytte mot overspenning i dette tilfellet er en avleder koblet til transformatorens nøytrale.

La overspenningsbølgen komme i tre faser Den ekvivalente kretsen til transformatoren samt forplantningen av den innfallende bølgen i transformatorviklingen er vist i figur 7.

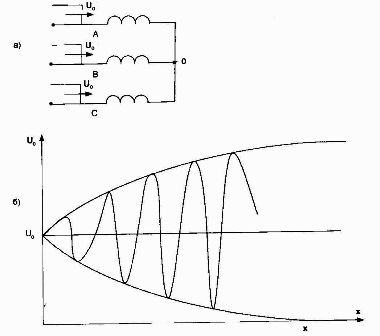
Figur 7.Ekvivalent krets av en trefase transformator med en stjernekoblet høyspenningsvikling (a) og avhengigheten U = f (x) for tilfellet når bølgen kommer i tre faser.

Forplantningsprosessene til en overspenningsfallbølge i hver av fasene til en trefasetransformator vil være lik prosessene i en enfasetransformator med isolert utgang. Den høyeste spenningen i denne modusen vil være i nøytral og vil være 2U0. Dette tilfellet av transformatoroverspenning er det mest alvorlige.

Trefase høyspent delta-viklet transformator

La overspenningsbølgen passere gjennom en fase A av en trefase høyspenttransformator koblet i et delta, de to andre fasene (B og C) anses som jordet (Figur 8).

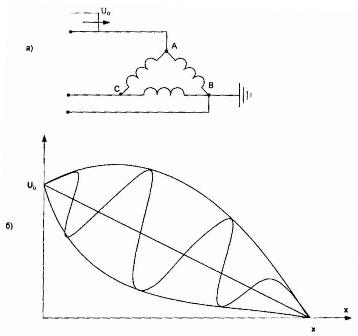
Figur 8. Ekvivalent krets av en trefase transformator med en høyspenningsvikling koblet i delta (a) og avhengigheten U = f (x) for tilfellet når bølgen kommer i en fase.

Viklinger AC og BC vil bli utsatt for en overspenning (1,3 — 1,4) Uo. Disse overspenningene er ikke farlige for driften av transformatoren.

La overspenningsbølgen komme i to faser (A og B), de forklarende grafene er vist i figur 9. I denne modusen vil forplantningen av overspenningsbølgene i viklingene AB og BC være lik prosessene i de tilsvarende viklingene til en trefase jordet transformatorterminal. Disse. i disse viklingene vil overspenningsverdien være (1,3 — 1,4) Uo og i AC-viklingen vil den nå verdien (1,8 — 1,9) Uo.

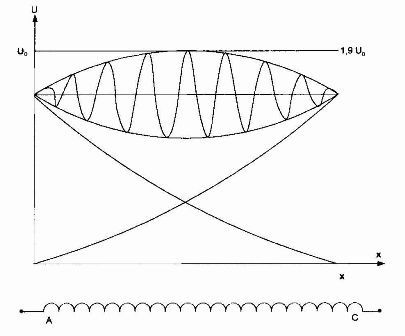
Figur 9. Avhengighet U = f (x) for tilfellet når overspenningsbølgen går gjennom to faser av en trefase transformator med en høyspentvikling koblet i delta.

La overspenningsbølger passere gjennom alle tre fasene til en trefasetransformator med en høyspent deltakoblet vikling.

Viklingene til alle fasene i denne modusen vil bli utsatt for en overspenning (1,8 - 1,9) Uo. Hvis en bølgebølge kommer samtidig gjennom to eller tre ledninger, kan det oppstå spenningssvingninger med en amplitude som er farlige for driften av transformatoren i midten av viklingen, som bølgene kommer fra begge sider.

Transformator overspenningsvern

De farligste overspenningene til hovedisolasjonen til viklingene kan oppstå ved samtidig ankomst av bølger gjennom tre ledninger til transformatoren med en deltaforbindelse (i midten av viklingen) eller en stjerne med en isolert nøytral (nesten nøytral) . I dette tilfellet nærmer amplitudene til de resulterende overspenningene to ganger spenningen til utgangen eller fire ganger amplituden til inngangsbølgen. Farlige sving-til-sving-isolasjonsoverspenninger kan oppstå i alle tilfeller når en bølge med en bratt front kommer til transformatoren, uavhengig av koblingsskjemaet til transformatorviklingene.

For alle transformatorer i tilfelle overspenninger og deres fordeling langs viklingene, for å estimere deres størrelse, er det derfor nødvendig å ta hensyn til kapasitansene i de ekvivalente kretsene til transformatorene (og ikke bare induktansen). Nøyaktigheten til de oppnådde overspenningsverdiene avhenger i stor grad av nøyaktigheten til kapasitansmålingen.

For å unngå overspenninger i utformingen av transformatorer, er det gitt:

• en ekstra skjerm som fordeler ladestrømmen, derfor reduseres overspenninger.Skjermen reduserer også feltstyrken på visse punkter på transformatorviklingen,

• styrke isolasjonen til viklingene i visse deler av den (konstruktiv erstatning av viklingene til transformatoren),

• installasjon av avledere foran og etter transformatoren — mot eksterne og interne overspenninger, samt en avleder i transformatorens nøytrale.