Uforgrenede og forgrenede lineære elektriske kretser med en enkelt forsyning
Hvis et stort antall passive elementer sammen med en kilde til f.eks. etc. c. danner en elektrisk krets, deres sammenkobling kan gjøres på forskjellige måter. Det er følgende typiske skjemaer for slike tilkoblinger.
Seriekobling av elementer Dette er den enkleste koblingen. Med denne forbindelsen flyter den samme strømmen i alle elementene i kretsen. I henhold til dette skjemaet kan enten alle de passive elementene i kretsen kobles til, og deretter vil kretsen være enkeltkrets uforgrenet (fig. 1., a), eller bare en del av elementene i flerkretskretsen kan være tilkoblet.
Hvis n elementer er koblet i serie der den samme strømmen I flyter, vil spenningen ved kretsens terminaler være lik summen av spenningsfallet i n elementer koblet i serie, dvs.
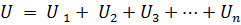
eller:
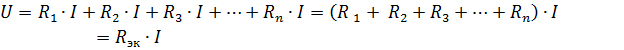
hvor Rek er ekvivalent kretsmotstand.
Derfor er den ekvivalente motstanden til passive elementer koblet i serie lik summen av motstandene til disse elementene ... Det elektriske skjemaet (fig.1, a) kan en ekvivalent krets presenteres (fig. 1, b), bestående av ett element med en ekvivalent motstand Rek
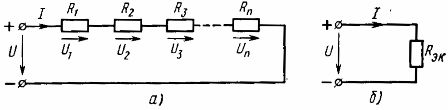
Ris. 1. Skjema for seriekobling av lineære elementer (a) og dets ekvivalente skjema (b)
Ved beregning av en krets med elementer koblet i serie ved en gitt spenning av strømkilden og motstandene til elementene, beregnes strømmen i kretsen i henhold til Ohms lov:
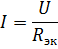
Spenningsfall over kth element
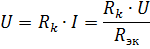
avhenger ikke bare av motstanden til dette elementet, men også av den ekvivalente motstanden Rek, det vil si motstanden til andre elementer i kretsen. Dette er en betydelig ulempe ved seriekobling av elementer. I det begrensende tilfellet, når motstanden til ethvert element i kretsen blir lik uendelig (åpen krets), blir strømmen i alle elementene i kretsen null.
Siden, når den er koblet i serie, er strømmen i alle elementene i kretsen den samme, er forholdet mellom spenningsfallet i elementene lik forholdet mellom motstandene til disse elementene:
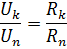
Parallell tilkobling av elementer - dette er en tilkobling der den samme spenningen påføres alle elementene i kretsen. I henhold til parallellkoblingsskjemaet kan enten alle passive elementer i kretsen (fig. 2, a) eller bare en del av dem kobles til. Hvert parallellkoblede element danner en separat gren. Derfor vil kretsen med parallellkobling av elementene vist i fig. 2, a, selv om det er en enkel krets (siden den inneholder bare to noder), er den samtidig forgrenet.
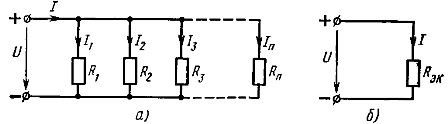
Ris. 2. Skjema for parallellkobling av lineære elementer (a) og tilsvarende skjema (b)
I hver parallellgren er strømmen
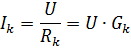
hvor Gk er ledningsevnen til den kth grenen.
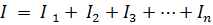
eller
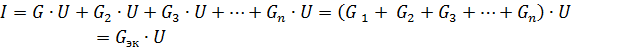
hvor Gec er ekvivalent kretskonduktans.
Derfor, når passive elementer er koblet parallelt, er deres ekvivalente konduktans lik summen av konduktansene til disse elementene... Ekvivalent konduktans er alltid større enn konduktansen til noen del av de parallelle grenene. Ekvivalent ledningsevne GEK tilsvarer ekvivalent motstand Rek = 1 / Gek.
Deretter den ekvivalente kretsen vist i fig. 2, a, vil ha den form som er vist i fig. 2, b. Strømmen i den uforgrenede delen av kretsen med parallellkobling av elementer kan bestemmes fra denne kretsen i henhold til Ohms lov:
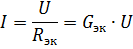
Derfor, hvis forsyningsspenningen er konstant, øker strømmen i den uforgrenede delen av kretsen (strømforsyningsstrømmen) med en økning i antall elementer koblet parallelt (som fører til en økning i ekvivalent ledningsevne).
Fra formelen
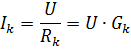
det kan sees at strømmen i hver gren bare avhenger av konduktansen til den grenen og ikke avhenger av konduktansen til andre grener. Uavhengigheten av parallelle grenmoduser fra hverandre er en viktig fordel ved parallellkobling av passive elementer. I industrielle installasjoner brukes i de fleste tilfeller parallellkobling av elektriske mottakere. Det mest åpenbare eksemplet er inkluderingen av elektriske lamper for belysning.
Siden i en parallellkobling påføres samme spenning til alle elementer og strømmen i hver gren er proporsjonal med konduktansen til den grenen, er forholdet mellom strømmer i parallelle grener lik forholdet mellom konduktansene til disse grenene, eller omvendt proporsjonal til forholdet mellom motstandene deres:
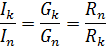
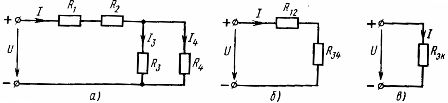
En blandet kobling av elementer er en kombinasjon av serie- og parallellkoblinger. En slik kjede kan ha et annet antall noder og grener. Et eksempel på en blandet tilkobling er vist i diagrammet (fig. 3, a)
Ris. 3. Skjema for blandet kobling av lineære elementer (a) og dets ekvivalente skjemaer (b, c).
For å beregne en slik krets, er det nødvendig å suksessivt bestemme de ekvivalente motstandene for de delene av kretsen som bare er serie- eller bare parallellkopling. I den betraktede kretsen er det en seriekobling av elementer med motstand R1 og R2 og en parallellkobling av elementer med motstand R3 og R4. Ved å bruke de tidligere oppnådde forholdene mellom parameterne til kretselementene med deres serie- og parallellkobling, kan den virkelige elektriske kretsen suksessivt erstattes av ekvivalente kretser.
Ekvivalent motstand av elementer koblet i serie
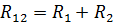
Ekvivalent motstand for parallellkoblede elementer R3 og R4
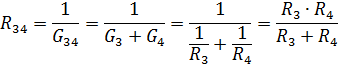
En ekvivalent krets med motstandene til elementene R12 og R34 er vist i fig. 3, b. For denne seriekoblingen av R12 og R34 er ekvivalent motstand
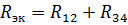
og den tilsvarende ekvivalente kretsen er vist i fig. 2, b. La oss finne strømmen i denne kretsen:
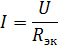
Dette er forsyningsstrømmen og strømmen i elementene R1 og R2 i den virkelige kretsen.For å beregne strømmene I3 og I4, bestemme spenningen i delen av kretsen med motstand R34 (fig. 3, b):
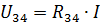
Da kan strømmene I3 og I4 finnes i henhold til Ohms lov:
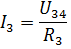
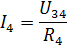
På lignende måte kan du beregne en rekke andre elektriske kretser med blandet kobling av passive elementer.
For komplekse kretser med et stort antall kretser og kilder til f.eks. etc. c. en slik tilsvarende ombygging kan ikke alltid gjennomføres. De beregnes etter andre metoder.