Impulsstrøm

I forskjellige elektroniske enheter, for eksempel i elektronisk utstyr og halvlederutstyr, det vil si i forsterkere, likerettere, radioer, generatorer, fjernsyn, så vel som i karbonmikrofoner, telegrafer og mange andre enheter, er de mye brukt krusningsstrømmer og spenninger... for ikke å gjenta resonnementet to ganger, vi vil bare snakke om strømmer, men alt som er relatert til strømmer er også sant for spenninger.

Pulserende strømmer som har en konstant retning, men som endrer verdien kan være forskjellige. Noen ganger endres gjeldende verdi fra den høyeste til den laveste verdien som ikke er null. I andre tilfeller reduseres strømmen til null. Hvis likestrømskrets blir avbrutt med en viss frekvens, så er det i noen tidsintervaller ingen strøm i kretsen.

I fig. 1 viser grafer av forskjellige bølgestrømmer. I fig. 1, a, b, skjer endringen i strømmer iht sinusformet kurve, men disse strømmene bør ikke betraktes som sinusformede vekselstrømmer, siden retningen (tegnet) til strømmen ikke endres. I fig.1 viser c en strøm som består av separate pulser, det vil si kortvarige "støt" av strøm, atskilt fra hverandre ved pauser av større eller mindre varighet, og kalles ofte pulserende strøm. Ulike pulserte strømmer skiller seg fra hverandre i formen og varigheten av pulsene, så vel som i repetisjonshastigheten.

Det er praktisk å betrakte en pulserende strøm av noe slag som summen av to strømmer - likestrøm og vekselstrøm, kalt term- eller komponentstrømmer. Enhver pulserende strøm har DC- og AC-komponenter. Dette virker merkelig for mange. Faktisk, tross alt, er en pulserende strøm en strøm som hele tiden flyter i én retning og endrer verdien.

Hvordan kan du se at den inneholder vekselstrøm som endrer retning? Men hvis to strømmer - direkte og vekselvis - passerer samtidig gjennom samme ledning, viser det seg at det vil flyte en pulserende strøm i den ledningen (fig. 2). I dette tilfellet bør amplituden til vekselstrømmen ikke overstige verdien av likestrømmen. Likestrøm og vekselstrøm kan ikke flyte separat gjennom ledningen. De legger til en generell strøm av elektroner som har alle egenskapene til en pulserende strøm.

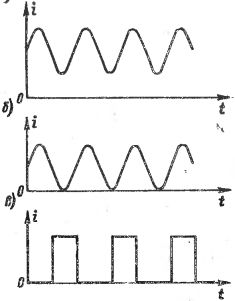
Ris. 1. Grafer over ulike bølgestrømmer

Tillegg av vekselstrøm og likestrøm kan vises grafisk. I fig. 2 viser grafene for en likestrøm lik 15 mA og en vekselstrøm med en amplitude på 10 mA. Hvis vi summerer verdiene til disse strømmene for individuelle punkter i tid, under hensyntagen til retningene (tegnene) til strømmene, får vi bølgestrømgrafen vist i fig. 2 med en fet linje. Denne strømmen varierer fra et lavt nivå på 5 mA til et maksimum på 25 mA.

Det betraktede tillegget av strømmer bekrefter gyldigheten av representasjonen av den pulserende strømmen som summen av likestrøm og vekselstrøm. Riktigheten av denne representasjonen bekreftes også av det faktum at ved hjelp av noen enheter er det mulig å skille komponentene til denne strømmen fra hverandre.

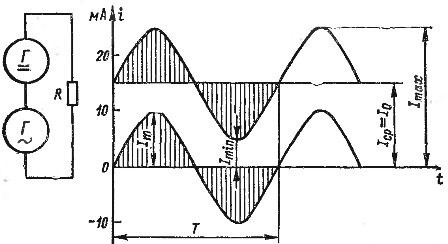
Ris. 2. Oppnå en pulserende strøm ved å legge til like- og vekselstrøm.

Det skal understrekes at enhver strøm alltid kan representeres som en sum av flere strømmer. For eksempel kan en strøm på 5 A betraktes som summen av strømmene 2 og 3 A som flyter i én retning, eller summen av strømmene 8 og 3 A som strømmer i forskjellige retninger, det vil si, med andre ord, forskjellen mellom strømmer 8 og 3 A. Det er ikke vanskelig å finne andre kombinasjoner av to eller flere strømmer som gir totalt 5 A.

Her er det en fullstendig likhet med prinsippet om addisjon og dekomponering av krefter. Hvis to like rettede krefter virker på en gjenstand, kan de erstattes med én felles kraft. Krefter som virker i motsatte retninger kan erstattes med en enhetsforskjell. Motsatt kan en gitt kraft alltid betraktes som summen av tilsvarende like rettede krefter eller differansen mellom motsatt rettede krefter.

Det er ikke nødvendig å dekomponere like- eller sinusformede vekselstrømmer til komponentstrømmer. Hvis vi erstatter den pulserende strømmen med summen av like- og vekselstrøm, så ved å bruke de kjente lovene for like- og vekselstrøm på disse komponentstrømmene, er det mulig å løse mange problemer og gjøre de nødvendige beregningene knyttet til pulserende strøm.

Konseptet med pulserende strøm som summen av likestrøm og vekselstrøm er konvensjonelt.Det kan selvsagt ikke antas at like- og vekselstrømmene i visse tidsintervaller virkelig flyter mot hverandre langs ledningen. Faktisk er det ikke to motsatte strømmer av elektroner.

I virkeligheten er en pulserende strøm en enkelt strøm som endrer verdien over tid. Det er mer riktig å si at den pulserende spenningen eller pulserende EMF kan representeres som summen av de konstante og variable komponentene.

For eksempel, i fig. 2 viser hvor algebraisk den konstante emk til en generator adderes til den variable emk til en annen generator. Som et resultat har vi en pulserende EMF som forårsaker den tilsvarende pulserende strømmen. Betinget kan det imidlertid betraktes at en konstant EMF skaper en likestrøm i kretsen, og en veksel-EMK - en vekselstrøm, som når den summeres, danner en pulserende strøm.

Hver pulserende strøm kan karakteriseres av maksimums- og minimumsverdiene til Itax og Itin, så vel som dens konstante og variable komponenter. Den konstante komponenten er betegnet med I0. Hvis vekselkomponenten er en sinusformet strøm, er dens amplitude betegnet med It (alle disse mengdene er vist i fig. 2).

Det må ikke forveksles med It og Itax. Den maksimale verdien av strømbølgen Imax bør heller ikke kalles amplituden. Begrepet amplitude refererer vanligvis bare til vekselstrømmer. Når det gjelder den pulserende strømmen, kan vi bare snakke om amplituden til dens variable komponent.

Den konstante komponenten av den pulserende strømmen kan kalles dens gjennomsnittsverdi Iav, det vil si den aritmetiske gjennomsnittsverdien. Faktisk, hvis vi vurderer endringene i en periode av den pulserende strømmen vist i fig.2, er følgende tydelig sett: i den første halvsyklusen legges en rekke verdier til 15 mA-strømmen ved å variere strømkomponenten, variere fra 0 til 10 mA og tilbake til 0, og i andre halvdel -syklus, nøyaktig de samme strømverdiene trekkes fra gjeldende 15 mA.

Derfor er strømmen på 15 mA egentlig gjennomsnittsverdien. Siden strøm er overføringen av elektriske ladninger gjennom tverrsnittet av ledningen, så er Iav verdien av en slik likestrøm som i en periode (eller i et helt antall perioder) bærer samme mengde elektrisitet som denne pulserende strømmen .

For sinusformet vekselstrøm er verdien av Iav per periode null fordi mengden elektrisitet som passeres gjennom tverrsnittet av lederen i en halvperiode er lik mengden elektrisitet som passerer i motsatt retning i løpet av en annen halvperiode. På grafene over strømmer som viser avhengigheten av strøm i på tid t, uttrykkes mengden elektrisitet som strømmen bærer av arealet av figuren avgrenset av strømkurven, siden mengden elektrisitet bestemmes av produkt som det.

For en sinusformet strøm er arealene til de positive og negative halvbølgene like I den pulserende strømmen vist i fig. 2, i løpet av den første halve perioden legges mengden elektrisitet som bæres av AC-komponenten til mengden elektrisitet som bæres av gjeldende Iav (skravert område i figuren). Og i løpet av andre halvsyklus trekkes nøyaktig samme mengde strøm ut. Som et resultat overføres samme mengde elektrisitet gjennom hele perioden som med en enkelt likestrøm Iav, det vil si at arealet av rektangelet Iav T er lik arealet avgrenset av bølgestrømkurven.

Dermed bestemmes den konstante komponenten eller gjennomsnittsverdien av strømmen av overføringen av elektriske ladninger gjennom tverrsnittet av ledningen.

Den nåværende ligningen vist i fig. 2 skal åpenbart skrives i følgende form:

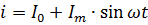
Effekten til den pulserende strømmen må beregnes som summen av kraftene til dens komponentstrømmer. For eksempel, hvis strømmen vist i fig. 2, går gjennom en motstand med motstand R, så er dens kraft

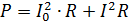
hvor I = 0.7Im er rms-verdien til den variable komponenten.

Du kan introdusere konseptet med rms-verdien til bølgestrømmen Id. Effekten beregnes på vanlig måte:

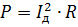
Ved å likestille dette uttrykket med det forrige og redusere det med R, får vi:

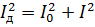
De samme relasjonene kan oppnås for stress.