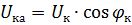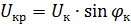Transformator kortslutningsmodus

Kortslutningsmodusen til transformatoren er en slik modus når terminalene til sekundærviklingen er lukket av en strømleder med en motstand lik null (ZH = 0). En kortslutning av transformatoren under drift skaper en nødmodus, siden sekundærstrømmen, og derfor primærstrømmen, øker flere titalls ganger sammenlignet med den nominelle. Derfor er det i kretser med transformatorer gitt beskyttelse som automatisk slår av transformatoren ved kortslutning.

Under laboratorieforhold er det mulig å utføre en testkortslutning av transformatoren, der terminalene til sekundærviklingen kortsluttes, og en spenning Uk påføres primærviklingen, der strømmen i primærviklingen gjør det. ikke overskride den nominelle verdien (Ik < I1nom). I dette tilfellet er spenningen Uk, uttrykt i prosent, med Ik = I1nom, betegnet med uK og kalles kortslutningsspenningen til transformatoren. den karakteristisk for transformatorenangitt i passet.

Dermed (%):

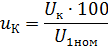
hvor U1nom er nominell primærspenning.

Kortslutningsspenningen avhenger av den høyere spenningen til transformatorviklingene. For eksempel, ved en høyere spenning på 6-10 kV uK = 5,5 %, ved 35 kV uK = 6,5 ÷ 7,5 %, ved 110 kV uK = 10,5 %, etc. Som du kan se, når merkespenningen øker, øker kortslutningsspenningen til transformatoren.

Når spenningen Uc er 5-10 % av den nominelle primærspenningen, synker magnetiseringsstrømmen (ubelastet strøm) 10-20 ganger eller enda mer betydelig. Derfor, i kortslutningsmodus anses det som

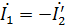
Den magnetiske hovedfluksen F avtar også med en faktor 10–20, og lekkasjestrømmene til viklingene blir i samsvar med hovedfluksen.

Siden når sekundærviklingen til transformatoren er kortsluttet, er spenningen på terminalene U2 = 0, f.eks. etc. s. fordi det tar formen

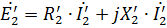
og spenningsligningen for transformatoren skrives som

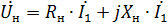
Denne ligningen tilsvarer transformatorekvivalentkretsen vist i fig. 1.

Vektordiagrammet til kortslutningstransformatoren som tilsvarer ligningen og diagrammet i fig. 1 er vist i fig. 2. Kortslutningsspenning har aktive og reaktive komponenter. Vinkelen φk mellom vektorene til disse spenningene og strømmene avhenger av forholdet mellom de aktive og reaktive induktive komponentene til transformatormotstanden.

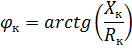
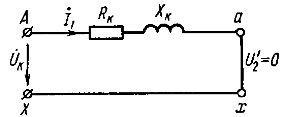
Ris. 1. Ekvivalent krets for transformatoren ved kortslutning

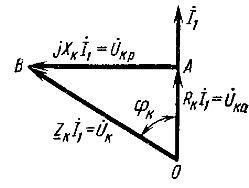
Ris. 2. Vektordiagram av transformatoren under kortslutning

For transformatorer med merkeeffekt 5-50 kVA XK / RK = 1 ÷ 2; med merkeeffekt 6300 kVA eller mer XK / RK = 10 eller mer. Derfor antas det at for høyeffekttransformatorer UK = Ucr og impedansen ZK = Xk.

Kortslutningsopplevelse.

Dette eksperimentet, i likhet med tomgangseksperimentet, utføres for å bestemme parametrene til transformatoren. En krets er satt sammen (fig. 3) der sekundærviklingen er kortsluttet av en metall jumper eller ledning med motstand nær null. En spenning Uk påføres primærviklingen, ved hvilken strømmen i den er lik den nominelle verdien I1nom.

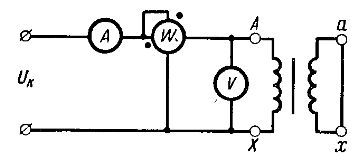
Ris. 3. Skjematisk av transformatorkortslutningsforsøket

I henhold til måledataene bestemmes følgende parametere for transformatoren.

Kortslutningsspenning

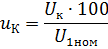
hvor UK er spenningen målt med et voltmeter ved I1, = I1nom I kortslutningsmodus er UK veldig lite, så tomgangstapene er hundrevis av ganger mindre enn ved nominell spenning. Dermed kan vi anta at Ppo = 0 og effekten målt av wattmeteret er effekttapet Ppk, på grunn av den aktive motstanden til transformatorviklingene.

Ved strøm I1, = I1nom få nominelle effekttap for oppvarming av viklingene Rpk.nom, som kalles elektriske tap eller kortslutningstap.

Fra spenningsligningen for transformatoren, samt fra den ekvivalente kretsen (se fig. 1), får vi

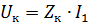
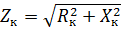
hvor ZK er impedansen til transformatoren.

Ved å måle Uk og I1 kan du beregne transformatorimpedans

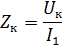
Strømtapet under en kortslutning kan uttrykkes med formelen

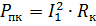
Derfor aktiv motstand til transformatorviklingene

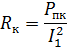
funnet fra watt- og amperemeteravlesningene. Når du kjenner Zk og RK, kan du beregne den induktive motstanden til viklingene:

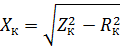
Når du kjenner Zk, RK og Xk til transformatoren, kan du bygge kortslutningsspenningene til hoveddeltaet (trekant OAB i fig. 2), og også bestemme de aktive og induktive komponentene til kortslutningsspenningen: