Tap og spenningsfall - hva er forskjellene

I vanlig menneskeliv brukes ordene "tap" og "fall" for å betegne det faktum at visse prestasjoner reduseres, men de betyr en annen verdi.

I dette tilfellet betyr «tap» tap av en del, skade, reduksjon av størrelsen på det tidligere oppnådde nivået. Tap er uønsket, men du kan tåle dem.

Ordet "fall" forstås som en mer alvorlig skade forbundet med fullstendig fratakelse av rettigheter. Dermed kan selv sporadisk forekommende tap (for eksempel en portefølje) over tid føre til en nedgang (for eksempel nivået på materiell levetid).

I denne forbindelse vil vi vurdere dette spørsmålet i forhold til spenningen til det elektriske nettverket.

Hvordan tap og spenningsfall dannes

Elektrisitet føres over lange avstander med luftledninger fra en nettstasjon til en annen.

Luftledninger er designet for å overføre tillatt kraft og er laget av metalltråder av et bestemt materiale og seksjon. De skaper en resistiv belastning med en motstandsverdi på R og en reaktiv belastning på X.

På mottakersiden står den transformatorstrømkonvertering.Spolene har en aktiv og uttalt induktiv motstand XL. Sekundærsiden av transformatoren senker spenningen og overfører den videre til forbrukerne, hvis belastning er uttrykt med verdien av Z og er aktiv, kapasitiv og induktiv av natur. Dette påvirker også de elektriske parametrene til nettverket.

Spenningen påført ledningene til støtten til luftledningen, nærmest kraftoverføringsstasjonen, overvinner den reaktive og aktive motstanden til kretsen i hver fase og skaper en strøm i den, hvis vektor avviker fra vektoren til kretsen. påført spenning med en vinkel φ.

Naturen til fordelingen av spenninger og strømmen av strøm langs linjen for en symmetrisk belastningsmodus er vist på bildet.

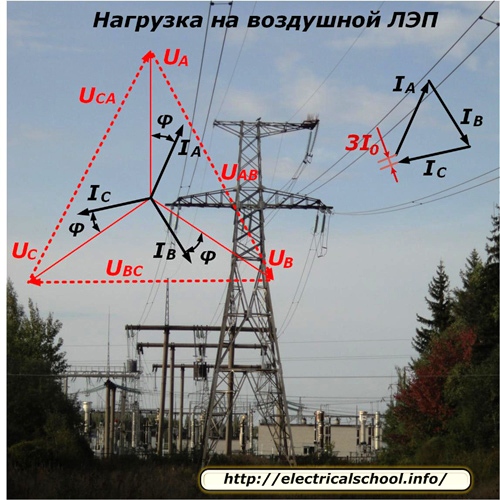
Siden hver fase av linjen mater et annet antall forbrukere som også er tilfeldig frakoblet eller koblet til arbeid, er det teknisk svært vanskelig å balansere fasebelastningen perfekt. Det er alltid en ubalanse i den, som bestemmes av vektortilsetningen av fasestrømmene og skrevet som 3I0. I de fleste beregninger blir det rett og slett ignorert.

Energien som forbrukes av den sendende transformatorstasjonen brukes delvis på å overvinne motstanden til linjen og når mottakersiden med liten endring. Denne fraksjonen er preget av tap og spenningsfall, hvis vektor avtar litt i amplitude og forskyves med en vinkel i hver fase.

Hvordan tap og spenningsfall beregnes

For å forstå prosessene som foregår under overføring av elektrisitet, er vektorformen praktisk for å representere hovedkarakteristikkene. Ulike matematiske beregningsmetoder er også basert på denne metoden.

For å forenkle beregningene i trefasesystem den er representert av tre enfase-ekvivalente kretser. Denne metoden fungerer godt med en symmetrisk belastning og lar deg analysere prosessene når den er ødelagt.

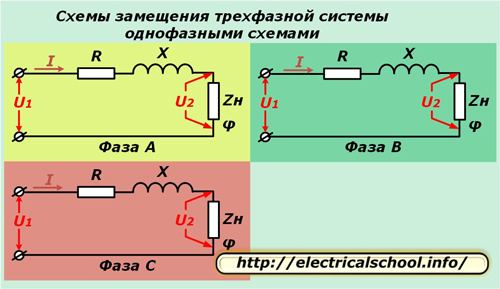
I diagrammene ovenfor er den aktive R og reaktansen X til hver leder av linjen koblet i serie med den komplekse lastmotstanden Zn karakterisert ved vinkelen φ.

I tillegg utføres beregning av spenningstap og spenningsfall i en fase. For å gjøre dette må du spesifisere dataene. For dette formålet velges en nettstasjon som mottar energi, hvor tillatt belastning allerede må bestemmes.

Spenningsverdien til et hvilket som helst høyspentsystem er allerede angitt i referansebøkene, og motstandene til ledningene bestemmes av deres lengde, tverrsnitt, materiale og konfigurasjon av nettverket. Den maksimale strømmen i kretsen er satt og begrenset av egenskapene til ledningene.

Derfor, for å starte beregningene, har vi: U2, R, X, Z, I, φ.

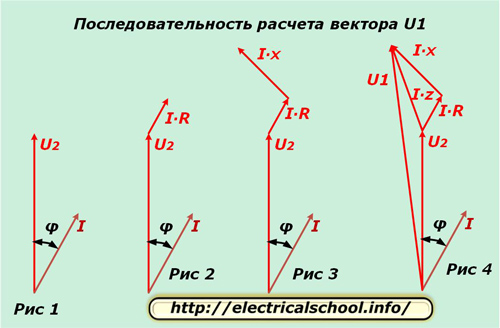
Vi tar en fase, for eksempel «A» og skiller for den i det komplekse planet vektorene U2 og I, forskjøvet med en vinkel φ, som vist i figur 1. Potensialforskjellen i den aktive motstanden til lederen faller sammen i retningen med strømmen og i størrelse bestemmes fra uttrykket I ∙ R. Vi utsetter denne vektoren fra slutten av U2 (fig. 2).

Potensialforskjellen i reaktansen til lederen er forskjellig fra strømmens retning med en vinkel φ1 og beregnes fra produktet I ∙ X. Vi utsetter det fra vektoren I ∙ R (fig. 3).

Påminnelser: for den positive rotasjonsretningen til vektorene i det komplekse planet, tas bevegelsen mot klokken. Strømmen som flyter gjennom den induktive lasten forsinker den påførte spenningen med en vinkel.

Figur 4 viser plotting av potensialforskjellsvektorene på den totale ledningsmotstanden I ∙ Z og spenningen ved inngangen til kretsen U1.

Nå kan du sammenligne inngangsvektorene med den ekvivalente kretsen og på tvers av lasten. For å gjøre dette, sett det resulterende diagrammet horisontalt (fig. 5) og tegn en bue fra begynnelsen med radiusen til modulen U1 til den skjærer retningen til vektoren U2 (fig. 6).

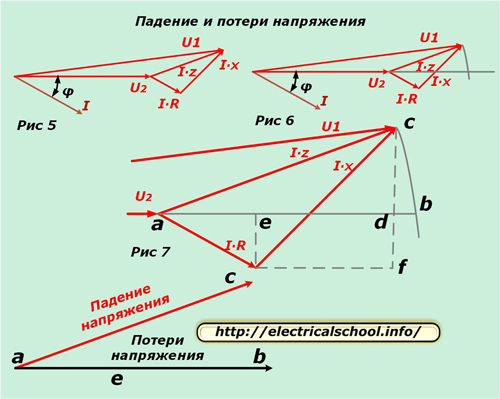
Figur 7 viser en forstørrelse av trekanten for større klarhet og tegning av hjelpelinjer, som indikerer de karakteristiske skjæringspunktene med bokstaver.

Nederst på bildet vises det at den resulterende vektoren ac kalles spenningsfallet og ab kalles tapet. De er forskjellige i størrelse og retning. Hvis vi går tilbake til den opprinnelige skalaen, vil vi se at ac oppnås som et resultat av geometrisk subtraksjon av vektorer (U2 fra U1), og ab er aritmetikk. Denne prosessen er vist på bildet nedenfor (fig. 8).

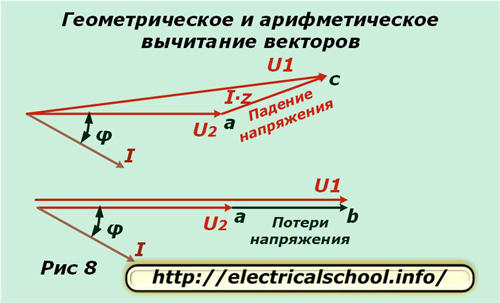
Utledning av formler for beregning av spenningstap

La oss nå gå tilbake til figur 7 og legge merke til at bd-segmentet er veldig lite. Av denne grunn neglisjeres det i beregningene og spenningstapet beregnes fra segmentlengden ad. Den består av to linjestykker ae og ed.

Siden ae = I ∙ R ∙ cosφ og ed = I ∙ x ∙ sinφ, kan spenningstap for en fase beregnes med formelen:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Hvis vi antar at lasten er symmetrisk i alle faser (betinget neglisjering av 3I0), kan vi bruke matematiske metoder for å beregne spenningstapet i ledningen.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Hvis høyresiden av denne formelen multipliseres og divideres med nettverksspenningen Un, så får vi en formel som lar oss utføre pBeregning av spenningstap gjennom strømforsyningen.

∆Ul = (P ∙ r + Q ∙ x) / Un

Verdiene for aktiv P og reaktiv Q-effekt kan hentes fra linjemåleravlesninger.

Dermed avhenger spenningstapet i en elektrisk krets av:

• aktiv og reaktans av kretsen;

• komponenter av anvendt kraft;

• størrelsen på den påførte spenningen.

Utledning av formler for beregning av den tverrgående komponenten av spenningsfallet

La oss gå tilbake til figur 7. Verdien av vektoren ac kan representeres ved hypotenusen til en rettvinklet trekant acd. Vi har allerede beregnet annonsefoten. La oss bestemme den tverrgående komponenten cd.

Figuren viser at cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Ved å bruke de oppnådde modellene utfører vi små matematiske transformasjoner og oppnår den tverrgående komponenten av spenningsfallet.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Bestemmelse av formelen for beregning av spenningen U1 ved begynnelsen av kraftledningen

Når vi kjenner verdien av spenningen på enden av linjen U2, tapet ∆Ul og den tverrgående komponenten til dråpen δU, kan vi beregne verdien av vektoren U1 ved Pythagoras teoremet. I utvidet form har den følgende form.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktisk bruk

Beregningen av spenningstap utføres av ingeniører på scenen for å lage et elektrisk kretsprosjekt for optimalt valg av konfigurasjonen av nettverket og dets bestanddeler.

Under drift av elektriske installasjoner, om nødvendig, kan samtidige målinger av spenningsvektorene ved endene av linjene utføres periodisk og resultatene oppnådd ved metoden for enkle beregninger kan sammenlignes. Denne metoden er egnet for enheter som har økt krav på grunn av behov for høy arbeidsnøyaktighet.

Spenningstap i sekundærkretser

Et eksempel er sekundærkretsene til målespenningstransformatorer, som noen ganger når flere hundre meter i lengde og overføres av en spesiell strømkabel med økt tverrsnitt.

De elektriske egenskapene til en slik kabel er underlagt økte krav til kvaliteten på spenningsoverføring.

Moderne beskyttelse av elektrisk utstyr krever drift av målesystemer med høye metrologiske indikatorer og en nøyaktighetsklasse på 0,5 eller til og med 0,2. Derfor må tap av spenningen som påføres dem overvåkes og tas i betraktning. Ellers kan feilen introdusert av dem i driften av utstyret påvirke alle operasjonelle egenskaper betydelig.

Spenningstap i lange kabellinjer

Funksjonen ved utformingen av den lange kabelen er at den har en kapasitiv motstand på grunn av det ganske nære arrangementet av ledende kjerner og et tynt lag med isolasjon mellom dem. Den avleder ytterligere strømvektoren som går gjennom kabelen og endrer størrelsen.

Effekten av spenningsfall på kapasitiv motstand må tas med i beregningen for å endre verdien av I ∙ z. Ellers endres ikke teknologien beskrevet ovenfor.

Artikkelen gir eksempler på tap og spenningsfall på luftledninger og kabler. Imidlertid finnes de hos alle forbrukere av elektrisitet, inkludert elektriske motorer, transformatorer, induktorer, kondensatorbanker og andre enheter.

Mengden av spenningstap for hver type elektrisk utstyr er lovlig regulert når det gjelder driftsforhold, og prinsippet for deres bestemmelse i alle elektriske kretser er det samme.